




Sie finden hier allgemeine Definitionen, Begriffserklärungen, Eigenarten der Funktionen,
Beschreibungen der verwendeten Funktionen, Verständnisbeispiele, Fehlermeldungen usw.
Werden Terme mit einem Argument außerhalb ihres Definitionsbereiches aufgerufen, so zeigt der
Rechner folgendes Verhalten:
- Taschenrechner:
Ein nicht zulässiges Argument führt zu einen Berechnungsabbruch. Eine
Fehlermeldung - wie z. B. „~ ist kein gültiger Gleitkommawert“ - wird
ausgegeben. Zur Fortsetzung der Rechnung muss der Zwischenspeicher
geleert werden, z. B. Doppelklick in das Eingabefeld.
Eine abgebrochene Rechnung kann durch copy (im Protokoll) and paste
(Eingabefeld) einfach korrigiert fortgeführt werden.
- Funktionenbereich: Damit ein versuchter Zugriff auf eine einzelne Funktion außerhalb ihres
Definitionsbereiches nicht zum Abbruch der aktuellen Gesamtoperation führen
kann, wird ein Einzelabbruch unterdrückt. So ist es z. B. möglich, dass die
Logarithmusfunktion x→ln(x) in einem Koordinatensystem, welches auch einen
negativen Abszissenabschnitt enthält, in ihrem Definitionsbereich geplottet
werden kann.
Funktionen - Eigenarten
Es werden hier anwendungsbezogen zwischen zwei Arten von Funktionen unterschieden:
1. Funktionen mit einem Argument wie sin(x), ln(x) usw.
2. Funktionen mit mehreren Argumenten wie log(x|b), B(n|p|k) usw.
Jede Funktion mit einem Argument kann als Argument auch Terme (inkl. Funktionen,
siehe oben) beinhalten!
usw.
Beispiel: Kreisfunktionen (mit a=1):
x → sqt( 1 – x^2 ) bzw.
x → (1–x^2 )^0,5 bzw.
x → (1-x^2)^(1/2) usw.
Achtung: Für Funktionen mit mehreren Argumenten sind Funktionen bzw. zusammengesetzte Terme
als Argumente nur im Programmbereich „f:x->f(x)“ möglich.
Einige Funktionen sind nur im Rahmen einer Programmierung sinnvoll. Hieraus ergibt
sich die folgende Deklaration:
Allgemeine Funktionen
Trigonometrische Funktionen
Umkehrfunktionen Arkus... (z. B. Arkussinus)
Hyperbelfunktionen ... hyperbolicus (z. B. Sinus hyperbolicus)
Umkehrfunktionen Area...(z. B. Areasinus hyperbolicus)
Anmerkung: Hyperbelfunktionen lassen sich (wie trigonometrische Funktionen am
Einheitskreis) an der Einheitshyperbel geometrisch herleiten.
Potenzfunktion
Hinweis: Die allgemeine Potenzfunktion f: x→f(x) = b^x kann mit gültiger Basis b in ihrem
Definitionsbereich immer verwendet werden.
Logarithmische Funktionen
Der Taschenrechner besitzt mehrere Möglichkeiten der Fehlerhinweise.
•
Ausgabe von Fehlerhinweises durch sich öffnende Fehlerfenster.
Im Ein- Ausgabefeld kann dann noch ein Zwischenwert stehen.
•
Im Ein- Ausgabefeld wird das Fehlerzeichen ~ ausgegeben.
•
Ein ungültiger Term wird im Register angezeigt, das Ein- Ausgabefeld bleibt leer.
Die Fehlerposition im eingegebenen Ausdruck (copy and paste) kann anhand der Registerangaben
bzw. des Protokolls ermittelt werden.
Nach einer Fehlermeldung müssen die Register mittels der Clear-Taste gelöscht werden!
Dieses kann auch durch einen Doppelklick in das Ein- Ausgabefeld bzw. durch die Eingabe des
Zeichens # erfolgen.
Beispiel für eine Division durch 0:
In der nachgfolgenden Zahlenkolonne, die in das Eingabefeld kopiert werden soll, ist eine Division
durch 0 (9/0) enthalten.
7*3+2*0+1-21/3+9/0+2-13 → Eingabe durch copy and paste:
Entertaste bzw. Button „=“
Die Zahl 15 im Registerfeld entspricht dem aktuellen Wert bis zur Fehlerposition 9/0 → „~“
(7*3+2*0+1-21/3=15).
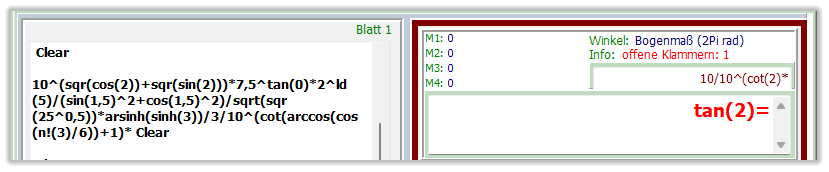
Beispiel für einen unvollständigen Term:
Beim Kopieren des Terms aus dem Beispiel für Kopiereingaben (siehe Beispiele 1) wurde die letzte
schließende Klammer nicht erfasst.
10^(sqr(cos(2))+sqr(sin(2)))*7,5^tan(0)*2^ld(5)/(sin(1,5)^2+cos(1,5)^2)/sqrt(sqr(25^0,5))*arsinh(sinh(3))/3/10^(cot(arccos(c
os(n!(3)/6))+1)*tan(2) )
Dieser Fehler, erkennbar am Gleichheitszeichen, wird auch in der Info-Zeile - Info:
offene Klammern: 1 - über dem Registerfenster angezeigt.
Nachfolgend weitere exemplarische Fehlerdarstellungen:
7+n!(3,1)-4 → Eingabe mit der Tastatur oder durch copy and paste:
Die Fehlerpositionen sind im Protokoll dargestellt.
Im Gegensatz zum klassischen Taschenrechner wurde für den Teilbereich „Funktionenrechner“ eine
Kalkulationsengine entwickelt, die auf den Prinzipien der Termumformungen basiert, siehe
„Entwicklungsgeschichte - Vierter Entwicklungsabschnitt“ (Pfeil unten, „Page n+1“).
Im Fehlerfall wird die aktuelle „Kompilierung“ abgebrochen und der verbleibende Fehlerterm wird im
Info-Fenster dargestellt. Dieses kann, insbesondere bei langen Formeln, zu nicht einfach zu
deutenden Fehlerinformationen führen.
Beispiel:
Im Term der Funktion f
1
wurde der Ausdruck … * Testfehler / ….. eingefügt.
Da das Programm den Begriff „Testfehler“ weder als Funktion noch als Konstante, Parameter usw.
einordnen konnte, wurde die Bearbeitung an dieser Stelle mit der obigen Fehlermeldung abgebro-
chen.
Die restlichen fehlerfreien Formeln können ausgegeben werden (Button Ja).
Praktischer Tipp:
Sollte einmal ein Funktionsgraph scheinbar nicht ausgegeben werden, kann mithilfe der Listenaus-
gabe der Wertebereich schnell überprüft werden. Auf eventuelle enthaltene Fehler wird dort ebenfalls
hingewiesen.


Abschnitt: Definitionsbereich
Abschnitt: Definitionsbereich
Abschnitt: Terme und Funktionen
Abschnitt: Terme und Funktionen

f: x → f( g( h(x) ) )
sin(x)
cos(x)
tan(x)
cot(x)
Abs( Term ):
liefert den positiven Wert des Terms.
sgn( Term ):
ist 1, wenn der Term positiv
(Term > 0) ist,
ist 0, wenn der Term = 0
(Term = 0) ist und
ist -1, wenn der Term negativ
(Term < 0) ist.
Mod(a|b):
ist -1, wenn der Term negativ
(Term < 0) ist. (a, b ∈ ℕ)
Sqr( Term ):
liefert den Quadratwert des Terms (square; x
2
).
sqrt( Term ):
liefert den Wurzelwert des Terms
(Term ∈ ℝ; Term ≥ 0)
(square root, x
0,5)
n!( Term ):
berechnet die Fakultät
(Term ∈ ℕ).
Bin(n|k):
berechnet den Binomialkoeffizient n über k.
(n, k ∈ ℕ).





arcsin(x)
arccos(x)
arctan(x)
arccot(x)

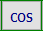

sinh(x)
cosh(x)
tanh(x)
coth(x)







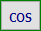
B(n|p|k):
Binomialverteilung
mit p ∈ ℝ, n, k ∈ ℕ
n: Anzahl der Versuche;
p: normale Wahrscheinlichkeit
k: Anzahl der erwarteten positiven Ereignisse
SB(n|p|[a;b]):
Binomial – Verteilungsfunktion
mit p ∈ ℝ, n, a, b ∈ ℕ
n: Anzahl der Versuche;
p: normale Wahrscheinlichkeit
a: kleinste Anzahl der erwarteten positiven Ereignisse
b: größte Anzahl der erwarteten positiven Ereignisse
( Abschnitt f:x→f(x): Im Gegensatz zur Lösungsvariablen x sind
Parameter usw. im Intervall [a;b] nicht zugelassen)
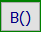
%:
Prozentrechnung
(% nicht programmierbar)
Funktion: Wert +(-*/^) x Prozent vom Wert = Ergebnis
Beispiele: 123 + 10
= 135,3
123 - 10
= 110,7
123 * 10
= 1512,9
123 / 10
= 10




--
cut( Term ):
schneidet die Nachkommastellen des Terms ab. Das Ergebnis ist
eine ganze Zahl.
--
round( Term ):
Rundet eine Kommazahl auf eine ganze Zahl.
exp(x)
(natürliche Exponentialfunktion, e-Funktion)

log(x|b)
Logarithmus von x zur Basis b
mit x,b∈ℝ; x,b>0; b≠1
ln(x)
Logarithmus zur Basis e, Logarithmus naturalis,
mit x∈ℝ; x>0
ld(x)
Logarithmus zur Basis 2, Logarithmus dualis
mit x∈ℝ; x>0
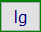
lg(x)
Logarithmus zur Basis 10, dekadischer Logarithmus
mit x∈ℝ; x>0


Definition: Terme
1.
Jede Zahl ist ein Term!
2.
Jede Variable oder Konstante ist ein Term!
3.
Jede Funktion ist in ihrem Definitionsbereich ein Term!
4.
Wenn T1 und T2 Terme sind, dann sind:
1. T1 + T2,
2. T1 - T2,
3. T1 * T2,
4. T1 : T2 (T2 ungleich 0)
5. T1 hoch T2,
auch Terme!

Hinweis Definitionsbereiche:
Falls ein Term (Funktion) als Argument Zahlen aus dem Bereich der ganzen Zahlen erwartet,
sind u. a. beispielsmäßig folgende Konstrukte möglich:
•
Definitionsbereich anpassen: x ∈ [a;b] mit a ∈ ℤ und Delta X ∈ ℕ vorgeben,
•
Argument konvertieren mit der Funktion cut(x) oder
•
Argument konvertieren mit der Funktion round(x).
Beispiele: Bin( 10 | Round(x) ) (Binomialkoeffizient n über k),
B( cut(x) | 0,2 | 20 ) (Bernoulli Formel).
Probiere: f
1
: n!( cut(x) ) und f
2
: n!( round(x) ) mit x ∈ [ -1,1 | 2,9 ] und y ∈ [ -1 | 7 ]

Hinweis Winkelwerte:
Bei Funktionen, deren Argument bzw. die sich selbst als Winkel darstellen, ist der
Wert abhängig von der Winkeleinstellung in der Taschenrechnermaske.
Demnach hat der Vollwinkel
- im (klassischen) Gradmaß 360°,
- im Bogenmaß 2Pi rad und
- im geodätischen Winkelmaß (Neugrad) 400 gon!
Die Voreinstellung ist das Bogenmaß.







arsinh(x)

arcosh(x)

artanh(x)

arcoth(x)
2. Funktionen, die nur für den (programmierbaren) Bereich „f:x->f(x)“ gelten:
2. Funktionen, die nur für den (programmierbaren) Bereich „f:x->f(x)“ gelten:
3. Funktionen, die sowohl für die Taschenrechnereingabe (mit obiger Einschränkung), als
auch für den (programmierbaren) Bereich „f:x→f(x)“ definiert sind:
3. Funktionen, die sowohl für die Taschenrechnereingabe (mit obiger Einschränkung), als
auch für den (programmierbaren) Bereich „f:x→f(x)“ definiert sind:
1. Funktionen, die nur bzw. hauptsächlich für den Bereich „Taschenrechner“ gelten:
1. Funktionen, die nur bzw. hauptsächlich für den Bereich „Taschenrechner“ gelten:


Abschnitt: Fehlermeldungen des Taschenrechners
Abschnitt: Fehlermeldungen des Taschenrechners











Abschnitt: Fehlermeldungen des Funktionenrechners
Abschnitt: Fehlermeldungen des Funktionenrechners
Fehlerbeispiele:
Fehlerbeispiele:


Fehlermeldungen
Fehlermeldungen
Abschnitt: Definierte Funktionen
Abschnitt: Definierte Funktionen
Taschenrechner - Funktionenrechner
Taschenrechner - Funktionenrechner

























