




Abschnitt: Ableitungskurven
Abschnitt: Ableitungskurven
Funktionen - Ableitungen
Funktionen - Ableitungen
Die Ableitungskurven werden näherungsweise berechnet und anschließend automatisch im Ausga-
befenster bzw. auf dem gesamten Bildschirm ausgegeben. Ein Ausgabewechsel ist jederzeit
möglich.
Durch das Anklicken eines der vier runden Buttons wird die Funktion gewählt, von der die drei
Ableitungen f‘, f‘‘ und f‘‘‘ gebildet werden sollen.
Bei den vier zur Auswahl stehenden Funktionen handelt es sich um die in den Funktionen-
eingabemasken vom User eingegebenen Funktionen.
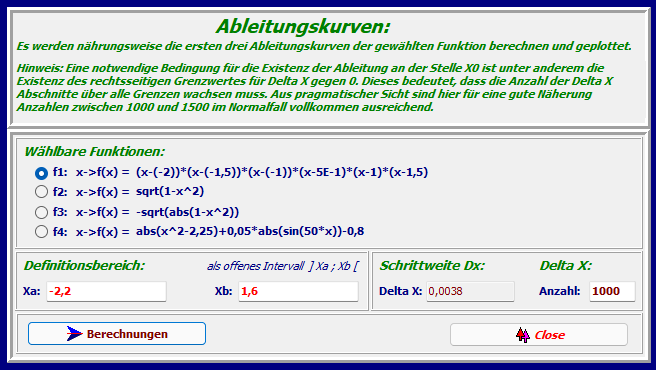
Der Definitionsbereich für die Funktionen kann hier festgelegt werden. Konstantenbezeichner
können ebenfalls verwendet werden.
Nach den Berechnungen mit den oben gewählten Optionen werden die Ergebnisse als Kurven
ausgegeben.
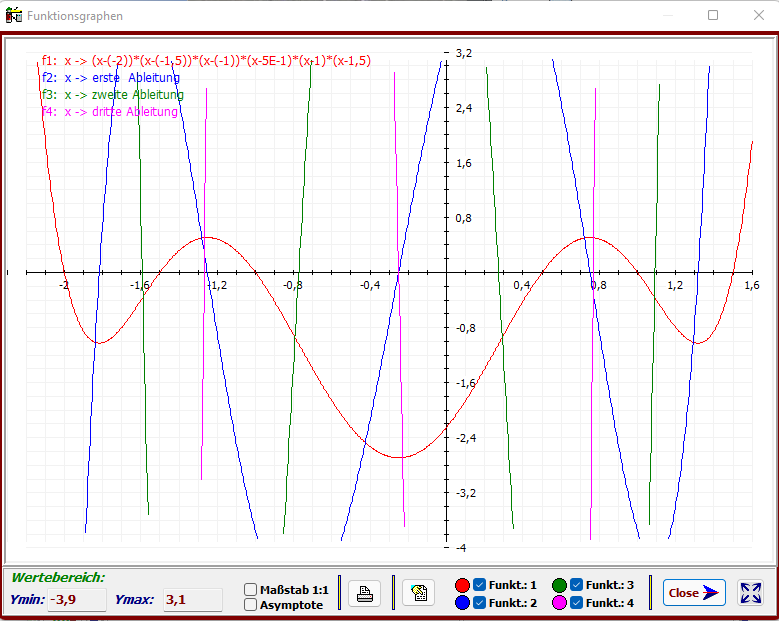
Bedingt durch den aktuellen Wertebereich y ∈ [ -3,9 | 3,1 ] werden die Ableitungsfunktionen nur
teilweise dargestellt.
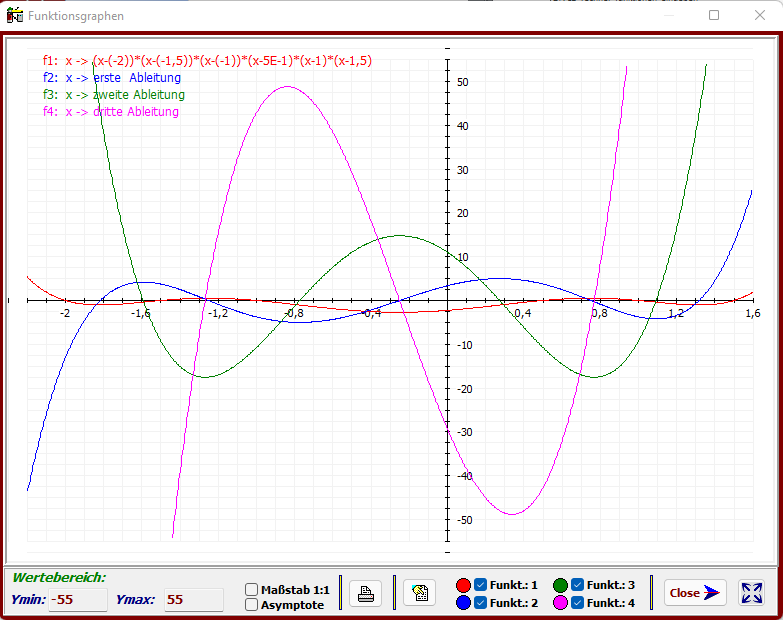
Die Darstellung lässt sich durch eine Änderung des Wertebereichs y ∈ [ -55 | 55 ] so anpassen, dass
alle drei Ableitungen (siehe oben) gezeigt werden können.
Wählbare Funktionen:
Wählbare Funktionen:
Ergebnis:
Ergebnis:
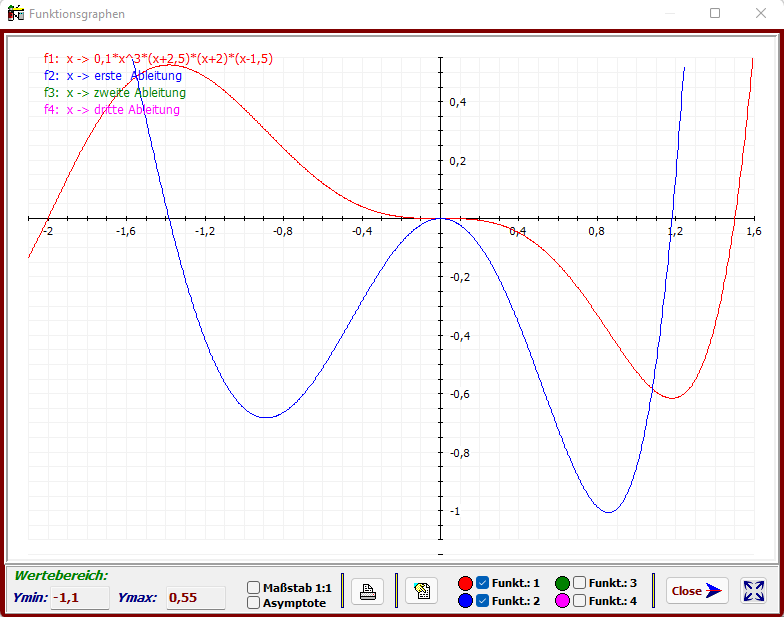
Als ein kleines einfaches Beispiel sei hier die (in ℝ differenzierbare) Funktion
f: x → f(x) = 0,1x
3
(x+2,5)(x+2)(x-1,5) im Bereich x ∈ [ -2,1 | 1,6 ] dargestellt.
Die Grafen der Ableitungsfunktionen (blau, grün, magenta) sind in der Menüleiste abgeschaltet.
Wie ersichtlich, besitzt die Funktion u. a. zwei Extremwerte und einen Wendepunkt im Ursprung.
Anhand der Kurve (rot) ist ersichtlich, dass in der Umgebungen des relativen Maximums
(Hochpunkt) gelten muss:
•
Der Funktionsgraf steigt bis zum Hochpunkt und fällt danach ab. Im Hochpunkt hat er eine
waagerechte Tangente.
Hieraus folgt für die Position ein rel. Maximum:
Die erste Ableitungsfunktion muss an dieser Abszissenposition fallend die Abszisse schneiden.
In Analogie zum rel. Maximum gilt für das rel. Minimum:
Für den Wendepunkt (im Ursprung) ist erkennbar, dass der fallende Kurvenverlauf (Steigung) der
(roten) Kurve immer flacher wird, um dann wieder permanent steiler zu werden. Das heißt, der
Funktionsgraf wechselt von einer Linksdrehung in eine Rechtsdrehung (L-R).
Für die erste Ableitungsfunktion f‘ (blau), die das Steigungsverhalten der Funktion f (rot) repräsen-
tiert, gilt, dass ihre Funktionswerte erst immer größer und dann wieder kleiner werden.
Die Ableitungsfunktion (blau) besitzt folglich an dieser Stelle ein rel. Maximum.
Der Extremwert der ersten Ableitungsfunktion f‘ (blau) entspricht der Steigung der Wendetangente.
Allgemein gilt: Eine Funktion hat einen Wendepunkt, wenn ihre Ableitungsfunktion an dieser Stelle
einen Extremwert (rel. Minimum bzw. rel. Maximum) besitzt.
Handelt es sich um ein rel. Maximum (blau, s.o.) so liegt ein Wendepunkt mit einem
Wechsel der Drehrichtung von links nach rechts (L-R) vor.
Bei einem rel Minimum gilt dann ein Wechsel von rechts nach links (R-L).
Hat die Wendetangente eines Wendepunktes einen waagerechten Verlauf, also m=0 (m=Steigung
bzw. m=tan(α)), dann bezeichnet man diesen Wendepunkt als Sattelpunkt.
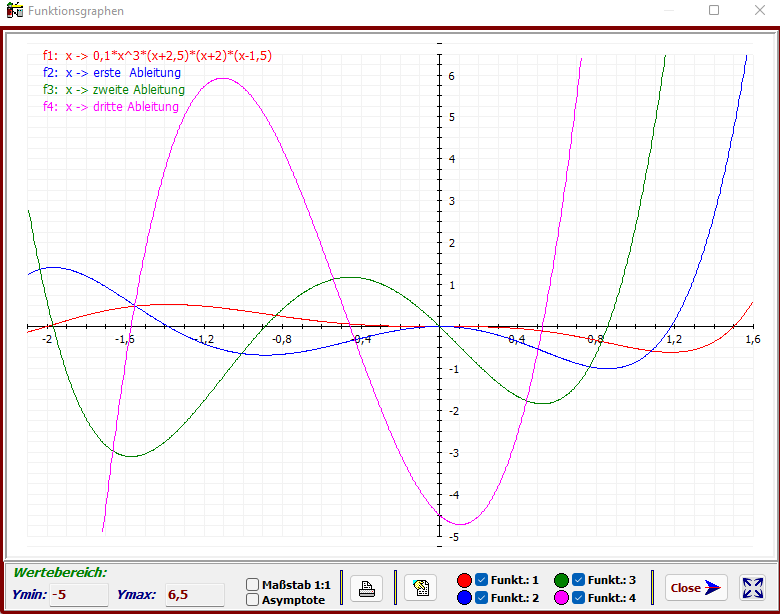
Die obige Abbildung zeigt alle Funktionsgrafen, es ist nun keine Funktion mehr ausgeblendet. Die
nachfolgend zusammengefassten Bedingungen lassen sich dort noch einmal anschaulich
verdeutlichen.
Die obigen Einschränkungen sind notwendig, da auch Extremwerte und Wendepunkte höherer
Ordnung existieren. So gelten zum Beispiel für die Parabeln:
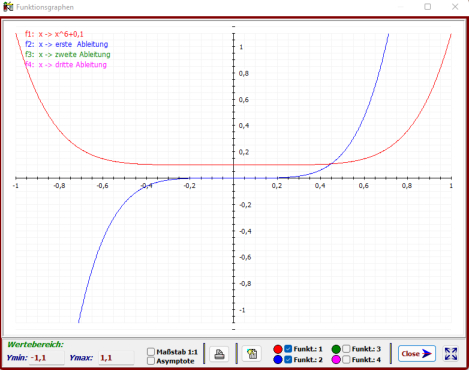
- f
1
: x → f(x) = x
6
+0,1 Die Parabel (gerader Ordnung) besitzt für x
0
= 0 ein rel. Minimum (linke Abb.).
Es gilt: f‘(0) = 0, f‘‘(0) = 0, f‘‘‘(0) = 0, f
IV
(0) = 0, f
V
(0) = 0, f
VI
(0) > 0
(erst die sechste Ableitung ist ungleich Null)
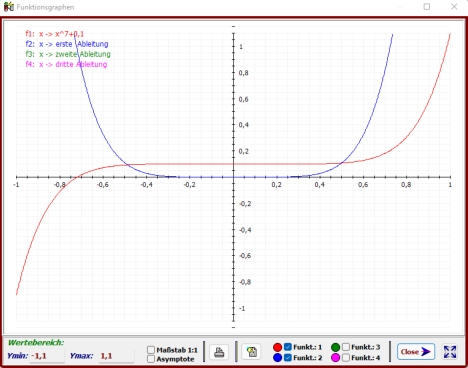
- f
2
: x → f(x) = x
7
+0,1 Die Parabel (ungerader Ordnung) besitzt für x
0
= 0 einen (R-L) Wendepunkt
(rechte Abb.).
Es gilt: f‘(0) = 0, f‘‘(0) = 0, f‘‘‘(0) = 0, f
IV
(0) = 0, f
V
(0) = 0, f
VI
(0) = 0, f
VII
(0) > 0
(erst die siebte Ableitung ist ungleich Null)
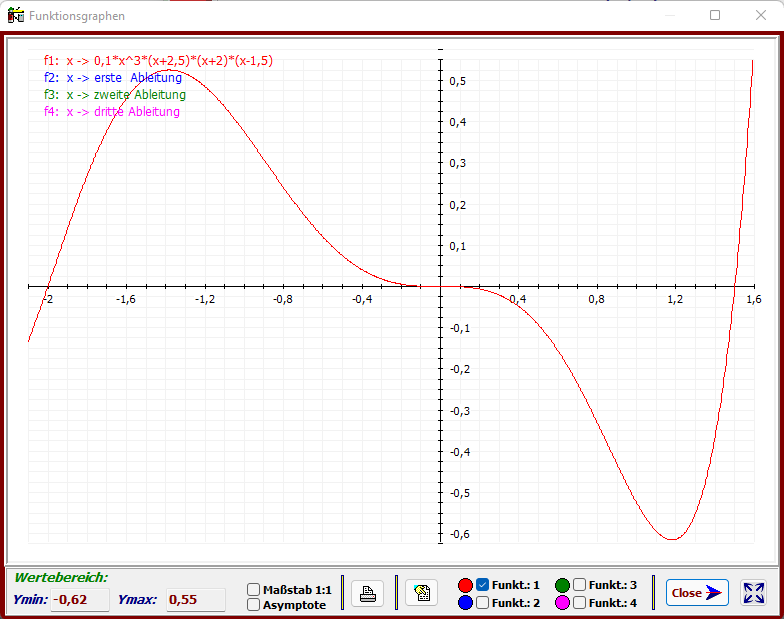
Kleines Beispiel:
Kleines Beispiel:


P
max
: f‘( x
max
) = 0 und f‘‘( x
max
) < 0; ( f‘‘<0 → fallend )

P
w
: f‘‘( x
w
) = 0 und f‘‘‘( x
w
) ≠ 0; f‘‘‘<0 → L-R; f‘‘‘>0 → R-L
Extremwerte
Extremwerte

Ein Wendepunkt
heißt Sattelpunkt, wenn zusätzlich gilt: f‘( x
w
) = 0


Allgemein gilt für Parabeln:
Ist die ersten Ableitung f
(n)
(x
w
) ( n ∈ ℕ ), die ungleich Null ist (f
(n)
(x
w
)≠0), eine Ableitung
- gerader Ordnung (n ist gerade Zahl), so handelt es sich um einen Extremwert,
- ungerader Ordnung (n ist ungerade), so handelt es sich um einen Wendepunkt.




P
min
: f‘( x
min
) = 0 und f‘‘( x
min
) > 0; ( f‘‘>0 → steigend )


Wendepunkte
Wendepunkte
Zusammenfassung:
Zusammenfassung:
Die Eingabemaske
Die Eingabemaske
Sattelpunkte:
Sattelpunkte:

























