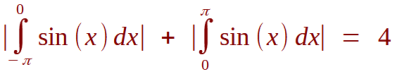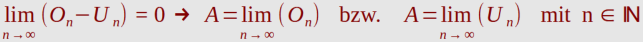Anwendungsbereich: Operationen mit Funktionen
Anwendungsbereich: Operationen mit Funktionen
Funktionen - Integrale
Funktionen - Integrale
Die näherungsweise Berechnungen der bestimmten Integrale erfolgen mithilfe der Riemannschen
Summe.
Verwendet werden hier die Ober- und Untersummen. Durch die Wahl der Anzahl der Abszissen-
punkte x
i
bzw. der Längen von Δx (Delta x) sowie der zugehörigen grafischen Darstellungen
(Obersummen, Untersummen u. Differenzsummen) können die Entwicklungen einfach und
übersichtlich nachvollzogen werden.
Bei den vier zur Auswahl stehenden Funktionen f1 .. f
4
handelt es sich um die in den Funktionen-
eingabemasken vom User eingegebenen Funktionen.
Der Definitionsbereich für die Funktionen ist nur für die Plotausgabe und begrenzt den grafischen
Darstellungsbereich. Dieses gilt auch für die zugehörige Stützpunkteanzahl.
Obwohl dieser Definitionsbereich keinen Einfluss auf die Berechnungen hat, sollte er immer etwas
größer sein als das Integrationsintervall.
Hier werden die Integrationsgrenzen a und b (Integral
von a nach b) eingegeben, über die die Integration er-
folgen soll. Konstantenbezeichner sind zulässig.
Die gewählte Anzahl der Stützpunkte (x
i
) bzw. der
Schrittweite Delta x ( Δx ) wirkt sich auf die Genau-
igkeit der Näherungsrechnungen aus.
Hinweis: Im Gegensatz zum Definitionsbereich müssen die Funktionen innerhalb der Integrations-
grenzen x∈[a;b] integrierbar sein.
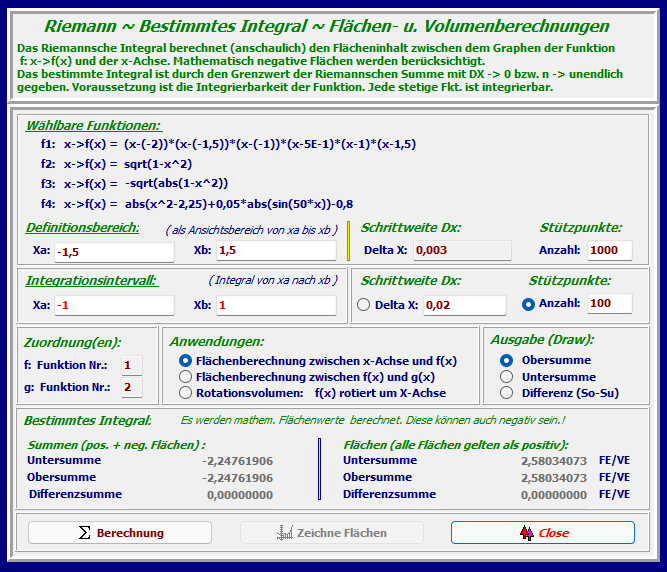
Hier werden aus dem oberen Pool („Wählbare Funktionen“) die Funktionen für die Funktion f und
die Funktion g gewählt, auf die im Bereich „Anwendungen“ bezug genommen wird.
Hier erfolgt die Wahl, ob die Funktion f in Verbindung mit der Abszisse, als Differenz in Verbindung
mit der Funktion g oder als Rotationskörper der Funktion f um die Abszissenachse berechnet
werden soll.
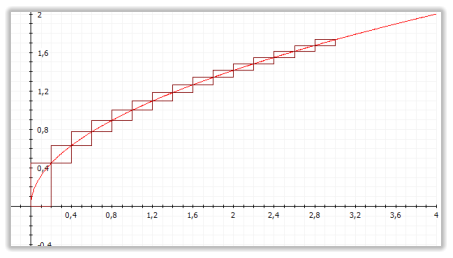
Sowohl die Untersummen- als auch die Obersummen- oder auch die
Differenzsummendarstellungen ( S
o
- S
u
) sind hier wählbar.
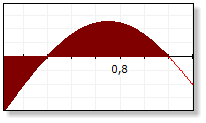
Die rechte Abbildung zeigt die Differenzsummenbildung.
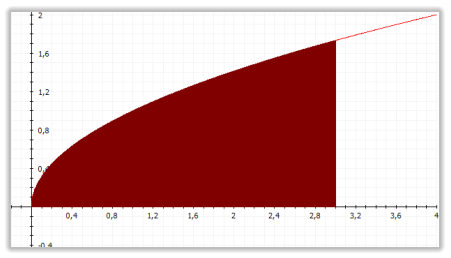
Das bestimmte Integral in den Grenzen von a nach b berechnet in der Summe alle Fläche zwischen
dem Funktionsgrafen und der Abszisse im vorgegebenen Intervall [a,b]. Hier sind die Flächen, die
sich oberhalb der Abszissenachse befinden, positiv und die Flächen unterhalb der Abszissenachse
negativ bewertet.
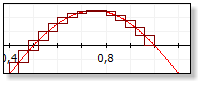
Beispiel: Für das Integral in den Grenzen von - Pi bis + Pi gilt:
bzw.
für die Fläche.
Die obigen Näherungen (Schrittzahl 1000) zeigen die Ergebnisse sowohl für das bestimmte Integral
von -Pi bis +Pi (Integral=0), als auch den Wert der tatsächlichen Fläche (hier gibt es keine negativen
Flächen) von -Pi bis +Pi an.
Die Berechnungen der Unter- und Obersummen erfolgen nach den folgenden Gesetzmäßig-
keiten.
Die Differenzsumme wird aus den beiden Summen gebildet D
n
= O
n
- U
n
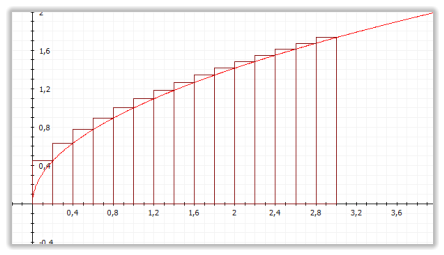
Dieses Beispiel soll die Zusammenhänge zwischen den Unter-, Ober- und Differenzsummen
anschaulich darstellen.
In den Grenzen von 0 und 3 sollen die Summen in Verbindung mit der Wurzelfunktion f: x → √x
gebildet werden.
Wie die beiden Summen zeigen, liegt die tatsächliche Flächengröße zwischen den beiden
Summenwerten.
Für die Fläche A gilt folglich die Ungleichung: U
n
≤ A ≤ O
n
Mit der obigen Ungleichung U
n
≤ A ≤ O
n
kann geschlossen werden:
und folglich für das bestimmte Integral:
Wie die nachfolgende näherungsweisen Rechnungen für n=15 zeigen, beträgt die Differenz der
beiden Summen D = 0,34641016.
Für n=10.000 reduziert sich die Differenzsumme auf 0,00051962.
Der arithmetische Mittelwert beträgt 3,46410054 FE
Zur Information: Der tatsächliche Flächeninhalt beträgt 3,4641 FE.
Der Fehler der obigen Näherungsrechnung liegt bei bei 5,4E-7, also ca. 0,000016%
Zuordnung der Funktionen f
1
und f
2
:
Zuordnung der Funktionen f
1
und f
2
:



Die Eingabemaske
Die Eingabemaske

Wählbare Funktionen:
Wählbare Funktionen:
Integrationsintervall:
Integrationsintervall:
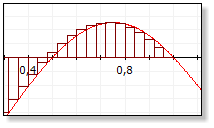
Anwendungen:
Anwendungen:
Ausgabe:
Ausgabe:
Bestimmtes Integral:
Bestimmtes Integral:
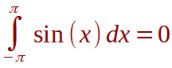

Untersumme - Obersumme - Differenzsumme:
Untersumme - Obersumme - Differenzsumme:
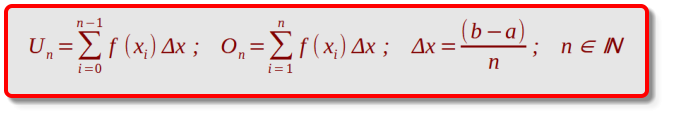
Beispiel:
Beispiel: