





Dieser Rechner für Funktionen ermöglicht es unter anderem,
a. Wertetabellen zu erstellen,
b. Funktionsgraphen zu plotten,
c. Riemannsche Summen zu plotten bzw. bestimmte Integrale zu berechnen,
d. Funktionsgraphen und die zugehörigen ersten drei Ableitungen grafisch
auszugeben,
e. Listen zu generieren usw.
Alle angeführten Beispiele können durch Kopieren und Einfügen (copy and paste) direkt im
Bereich „Funktioneneingabe“ in die Eingabefelder f
1
bis f
4
übernommen werden.
Die hier zu sehenden Screenshots der Plotausgaben sind zur besseren Wiedergabe (Skalierung
der Screenshots) bewusst nicht im Modus „Vollbildschirm“ erstellt worden.
Eine zusätzliche Druckausgabe der Ergebnisse ist immer möglich.
Bitte beachten Sie, dass nicht nur bei Übertragungskurven gerne logarithmische Abzisseneinteilungen
(halblogarithmische Darstellungen) benutzt werden. Die hier verwendeten Koordinatenteilungen sind linear.
Die hier gezeigten exemplarischen Beispiele demonstrieren nicht nur den universellen Rechner-
einsatz, sondern zeigen auch modifizierbare Lösungsstrategien im Umgang mit komplexen
Schaltungen.
Eingabehinweis: Ein Doppelklick im Eingabefenster löscht die akt. Eingabe.
Winkelein- und Ausgaben können auf drei Arten erfolgen (Bogenmaß, Altgrad, Neugrad;
siehe Hauptmaske „Taschenrechner“).
Da in der Elektrotechnik in Verbindung mit Phasengängen usw. oft im „Altgrad-
modus“ gerechnet wird, wählen Sie bitte in der Hauptmaske die Option
Winkeleinstellung „Grad“!
Um eine erstellte komplexe Formeln bezüglich der elektrischen Werte schnell variieren zu können,
werden gerne Parameter (Platzhalter) innerhalb der Formeln verwendet.
In Schaltungen werden z. B. oft mehrere Widerstände, Kondensatoren und Induktivitäten
verwendet. Hier könnte es vorteilhaft sein, allgemein über eine (eigene) Verwendungsordnung
nachzudenken.
In den Beispielen werden meistens für ohmsche Widerstände R die Parameter „R“ und „W“ und
bei Bedarf auch „U“ und „V“ , für elektrische Induktivitäten L die Parameter „L“ und „B“ und für
elektrische Kapazitäten C die Parameter „C“ und „A“ verwendet.
Beispiel: Verlustbehafteter Parallelschwingkreis:
|Z Parallel (x)| = { [( { [ 1 / W ] / [ 1/W^2 + { 2*Pi*x*C - 1/(2*Pi*x*L) }^2 ] } )^2] +
[( { [ 1 / (2*Pi*x*L) - 2*Pi*x*C ] / [ 1/W^2 + { 2*Pi*x*C - 1/(2*Pi*x*L) }^2 ] } )^2] }^0,5
Zugehörige Beispielparameterliste:
Empfehlung: Löschen Sie vor der Eingabe die Parameterliste (Doppelklick auf Mülltonne). Falls Sie
dann einen Parameter vergessen (oder fehlerhaft eingegeben) haben, erscheint nach
einer Plotausgabe in der Parameterliste ein Fehlerhinweis (????)!
Hier wurde kein Parameter eingetragen! Angezeigt werden alle verwendeten Parameter.
Falls mehrere Kurven mit großen unterschiedlichen Wertebereichen übersichtlich in einem
Koordinatensystem dargestellt werden sollen, ist es oft notwendig, Kurven dementsprechend zu
skalieren.
Dieses gilt hier oft für den Phasengang φ(f) mit φ(f)∈[ -180°; 180° ], der dem Ausgabewertebereich
Y ∈ [ -0,2; 1,2] angepasst werden soll. Hier ist eine Stauchung mit dem Faktor 0,001 notwendig.
f: x→f = c * ( φ(x) ); mit c=0,001 gilt: f: x→f = 0,001 * ( φ(x) ) Fehlerquelle: gesamten Term klammern!
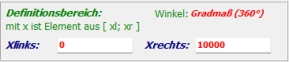
Die verwendeten Frequenzbereiche liegen i. Allg. zwischen 0 Hz
und 10 kHz. Sie werden jeweils im Definitionsbereich eingestellt.
(Entnehmen Sie hier die aktuellen Werte aus den Plotdarstellungen.)
Der Wertebereich kann jederzeit im Ausgabefenster in Echtzeit angepasst werden.
(Entnehmen Sie hier die aktuellen Werte aus den Plotdarstellungen.)
Die nachfolgenden Beispiele sollen die Möglichkeiten zeigen, auch komplexe technische Proble-
matiken relativ einfach (ohne aufwendige Versuchsdurchführungen) nur mittels physikalischer
Gesetzmäßigkeiten durch mathematisch erzeugten Kurven zu ergründen.
Die notwendigen Termumwandlungen werden hier übersichtlich fast rein formal durchgeführt.
Eine Optimierung ist nicht notwendig, da die Lösungsterme (in Abhängigkeit der Frequenz) vom
„Kleinen Taschenrechner“ ausgewertet werden sollen und dieser hinsichtlich der Formellänge
(praktisch) unbeschränkt ist.
Zum Ansatz kommen komplexe Zahlen in ihrer kartesischen Darstellungform. Ein abschnittsweiser
Wechsel zur Polarform kann den Rechnungsaufwand wesentlich verkürzen, insbesondere, wenn
die Real- und Imaginärteile des komplexen Gesamtwiderstandes usw. bereits vorliegen bzw.
berechnet worden sind. Dieses wird eindrucksvoll im Beispiel „Exponentialform: Beispiel LC -
Bandpass“ erläutert.
Die nachstehenden Beispiele eröffnen ein weites Feld zum Experimentieren mit modifizierten
Parametern und Werten. Sie ermöglichen es, die Fragen nach den Zusammenhängen in diesen
anspruchsvollen Bereichen der komplexen Bauelemente (inklusiv Phasenverschiebungen) zu
erforschen, zu durchdringen und vorhandene Erkenntnisse zu festigen. Dieses wäre sonst nur mit
aufwendigen und permanent zu modifizierenden Versuchsanordnungen möglich.
Die in den Beispielen entwickelten Formeln und Funktionen können direkt in die Eingabebereiche
des „Kleinen Rechners“ kopiert werden (copy and paste). Bei Funktionsgleichungen wird der linke
Teil incl. Gleichheitszeichen ignoriert.
(Hinweis: Die Pfeile dienen auch als Links!)
1. Übersicht - komplexe Rechnung:
Kurze Wiederholung einiger Grundlagen der komplexen Rechnung.
2. Beispiele - Kondensator und Spule:
Eigenschaften und Vergleich der idealen und der realen komplexen Bauelemente
Kondensator und Spule. Zur Darstellung und zum Vergleich der Kennlinien werden
die mathematischen Widerstandsfunktionen und Phasengänge ermittelt.
3. Beispiel Reihenschwingkreis:
Ermittlungen der komplexen idealen und realen Widerstandsfunktionen incl. der
Funktionen für die Phasengänge. Ein Vergleich erfolgt mittels der geplotteten
Kennlinien. Die Bezeichnung „Saugkreis“ lässt sich hier gut erläutern.
4. Beispiel Parallelschwingkreis:
Ermittlungen der komplexen idealen und realen Widerstandsfunktionen incl. der
Funktionen für die Phasengänge. Ein Vergleich erfolgt mittels der geplotteten
Kennlinien. Die Bezeichnung „Sperrkreis“ lässt sich hier gut erläutern.
5. Beispiel Reihen- und Parallelschwingkreise:
Ideale und reale Reihen- und Parallelschwingkreise werden hinsichtlich ihrer
Kennlinien bzw. Kurven gegenüber gestellt.
6. Beispiele Spannungsüberhöhungen:
Die Eigenschaft der Spannungsüberhöhung am Reihenschwingkreis kann, wenn sie
nicht bewusst gewollt ist, zu erheblichen Problemen führen.
Anhand der erstellten komplexen Verältnisfunktion U
e
/ U
a
(Übertragungsfunktion)
wird hier für U
a
eine um das 600-fache größere Spannung hinsichtlich der Eingangs-
spannung U
e
dokumentiert.
7. Beispiel: Tief- und Hochpass
Im Gegensatz zu einfachen RC bzw. RL Filter (Filter 1ter Ordnung) werden hier Filter
betrachtet, die aus Schwingkreise bestehen. Auch hier werden die Übertragungs-
funktionen incl. der Phasengangfunktionen erstellt und grafisch ausgewertet.
8. Beispiel: LC - Bandsperre
Im klassischen Ansatz erfolgt auch hier die formale Erstellung der schon aufwen-
digen Übertragungsfunktion. Auch hier kann das Verhalten der Bandsperre anhand
von wechselnden Parametern erforscht werden.
9. Beispiel: LC - Bandspass
In Analogie zur Bandpasssperre werden hier die Funktionsgleichungen erstellt und
mit unterschiedlichen Parameterwerten dargestellt.
10. Exponentialform: Beispiel LC - Bandpass
Die formale Berechnung der Übertragungsfunktion durch die ausschließliche
Verwendung der algebraischen Form führt zu einem hohen Rechenaufwand. Hier
wird der Vorteil der zusätzlichen Verwendung der Exponentialform gezeigt, die relativ
schnell und einfache zum Ergebnis führen kann.




Beispiele: Kondensator u. Spule
Beispiele: Kondensator u. Spule








Kurze Wiederholung einiger Grundlagen der komplexen Rechnung.
Kurze Wiederholung einiger Grundlagen der komplexen Rechnung.
Komplexe Rechnung
Komplexe Rechnung




Beispiel: Parallelschwingkreis
Beispiel: Parallelschwingkreis
Beispiel: Reihenschwingkreis
Beispiel: Reihenschwingkreis











Reihen- und Parallelschwingkreise
Reihen- und Parallelschwingkreise

















Beispiel: Spannungsüberhöhungen
Beispiel: Spannungsüberhöhungen









Rechner für Funktionen mit Variablen und Parametern.
Rechner für Funktionen mit Variablen und Parametern.
Exemplarische Beispiele mit kompexen Bauelementen
Exemplarische Beispiele mit kompexen Bauelementen
Beispieleverzeichnis (5):
Beispieleverzeichnis (5):

Rechner für Funktionen mit Variablen und Parametern.
Rechner für Funktionen mit Variablen und Parametern.
Beispielverzeichnis 5a
Beispielverzeichnis 5a
Beispielverzeichnis 5b
Beispielverzeichnis 5b





Winkelmodus:
Winkelmodus:


Parameterverwendungen:
Parameterverwendungen:


Funktionsgraphen skalieren (y-Achse):
Funktionsgraphen skalieren (y-Achse):
Abzisse (x-Achse):
Abzisse (x-Achse):
Ordinate (y-Achse):
Ordinate (y-Achse):
Hinweise für die hier vorgestellten Beispiele
Hinweise für die hier vorgestellten Beispiele
Die Erweiterung der reellen Zahlen mit die Menge der imaginären Zahlen führt zur Menge der
komplexen Zahlen.
Der reelle Term b wird als Imaginärteil bezeichnet, i als Imaginäre Einheit.
Aufgrund der Verwechselungsgefahr wird in der Elektrotechnik statt i der Buchstabe j verwendet.
Darstellungsformen:
1.
Algebraische Form (arithm., kartesische):
Z = a + ib
2.
Goniometrische Form:
Z = r(cos(φ)+isin(φ))
3.
Polarform, Exponentialform :
Z = re
iφ
Es gilt: r = |Z|
a = Re( Z ) = r cos(φ); b = Im( Z ) = r sin( φ )
φ = arctan( b / a ); φ = arctan( Im{ Z } / Re{ Z } )
Hinweis: Für den Wertebereich der Umkehrfunktion arctan(x) gilt: φ ∈ ] -90°; 90°[
Komplexen Größen, die einen Real- und einen Imaginärteil beinhalten, werden normalerweise
unterstrichen.
Komplexe Zahlen in der kartesischen Form
Komplexe Zahlen in der Polarform oder Exponentialdarstellung
Als klassische passive Grundelemente der Elektrotechnik sind hier sicherlich Widerstände,
Spulen und Kondensatoren zu nennen. Mathematisch können diese durch komplexe Ausdrücke
Für vereinfachte Formelerstellung hinsichtlich der Darstellungen von Widerstandskurven |Z(f)|,
Übertragungskurven |G(f)|, Frequenzgänge φ(f) usw. sind die nachfolgenden Formelgerüste
verwendbar.
Anmerkung: Die Tangensfunktion [ φ → tan(φ) ] hat an der Stelle φ = 90° einen Polsprung. Falls ein Realteil nicht
existiert, der Realteil = 0 (Re=0), ersetzen Sie Re durch einen sehr kleinen positiven Wert, z. B.:
arctan( Im / 1E-20 ) !
Im Formelgerüst können die Platzhalter Re und Im durch die Real- und Imaginärteile komplexer
Widerstandsfunktion, Übertragungsfunktion, Frequenzgangfunktionen usw. ersetzt werden. Die so
ergänzten Formeln können direkt kopiert und in eines der vier Eingabefelder (f
1
.. f
4
) eingefügt
werden.
Achtung: Für die Ausgaben der Frequenzgangkurven sollte der Rechner sich im
Modus „Gradmaß 360°“ befinden (Hautmaske)!
Der komplexe Gesamtwiderstand der Reihenschaltung ist gleich der Summe der komplexen
Einzelwiderstände.
Der komplexe Gesamtleitwert der Parallelschaltung ist gleich der Summe der komplexen
Einzelleitwerte.
mit Y = Z
-1
, G = Re Y und B = Im Y also Y = G + jB



Elektrotechnik
Elektrotechnik
Komplexe Bauelemente in der Elektrotechnik
Komplexe Bauelemente in der Elektrotechnik
Einige Grundrechenregeln:
Einige Grundrechenregeln:
Ohmscher Widerstand R
Ideale Spule
Idealer Kondensator



Der imaginäre Teil ist gleich 0
Z = R + j0 ⇔ Z = R
Der reale Teil ist gleich 0
Z = 0 + jX
L
⇔ Z = jωL
Der reale Teil ist gleich 0
Z = 0 + jX
C
⇔ Z = (-j)/(ωC)
Reihen und Parallelschaltungen von passiven Bauelementen
Reihen und Parallelschaltungen von passiven Bauelementen
Reihenschaltung:
Reihenschaltung:
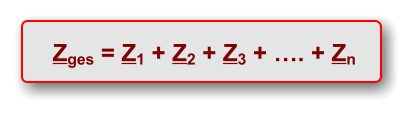
Parallelschaltung:
Parallelschaltung:
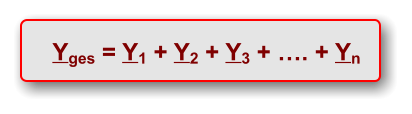

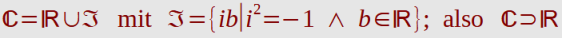


|Z(x)| = { [( Re )^2] + [( Im )^2] }^0,5


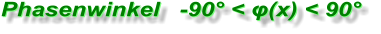
φ(x) = arctan[ ( Im ) / ( Re ) ] (mit Re ≠ 0)
Geometrische Darstellungen:
Geometrische Darstellungen:

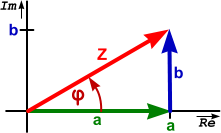
Grundsätzlich gibt es keine verlustfreien (passive) Bauelemente. Da die Rechnungen mit realen
Bauelementen oft sehr aufwendig und in dieser Form nicht immer notwendig sind, ist von Fall zu
Fall zu entscheiden, ob nicht eine Rechnung mit idealen (verlustfreien) Bauteilen ausreichende
Ergebnisse liefern.
Exemplarisch ist hier eine Ersatzschaltung für einen realen Kondensator dargestellt. Eine derartige
Betrachtung ist wohl eher in der Hochfrequenztechnik ((Ultra High Frequency, Super High
Frequency) von Bedeutung.
R
isol
:
Isolationswiderstand
R
ESR
:
ohmschen Anteile (z. B. Drähte, Kontakte usw.)
R
leak
:
Reststrom (z. B. Elko)
L
ESL
:
Induktivität (z. B. Wickelkondensator)
Induktive Widerstände können in vielen Fällen vereinfacht als Reihenschaltung einer idealen Spule
und einem ohmschen Widerstand (Drahtwiderstände usw.) dargestellt werden.
R
L
= Ohmscher Widerstand der Wicklungen usw.
X
L
= Induktiver Widerstand (Blindwiderstand)
Ideale Spulen besitzen nur den Blindwiderstand X
L
. Der Realteil ist gleich 0.
Variable x = f, Parameter L = L [H]
f
1
: |Z(x)| = {[( 0 )^2] + [( 2*Pi*x*L )^2]}^0,5
f
2
: φ(x) = 90° (reiner induktiver Widerstand; Realteil ist 0)f
1
:
Reale Spulen besitzen besonders in der Hochfrequenztechnik zusätzlich zum eigentlichen
induktiven Widerstand weiter Größen wie Eisenverluste, Drahtverluste, Parallelkapazitäten usw.
Im Normalfall reicht es aus, die ohmschen Widerstände in R
L
zusammen zu fassen.
Variable x = f, Parameter R = R
L
[Ω]; L = L [H];
f
3
: |Z(x)| = {[( R )^2] + [( 2*Pi*x*L )^2]}^0,5
f
4
: φ(x) = arctan[ ( 2*Pi*x*L ) / ( R ) ] (Winkeleinstellung: Altgrad (360°))
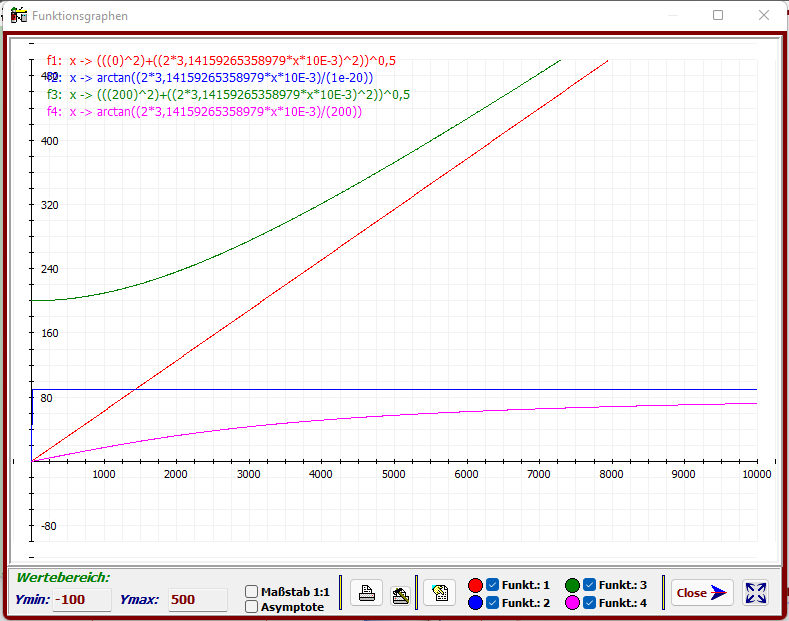
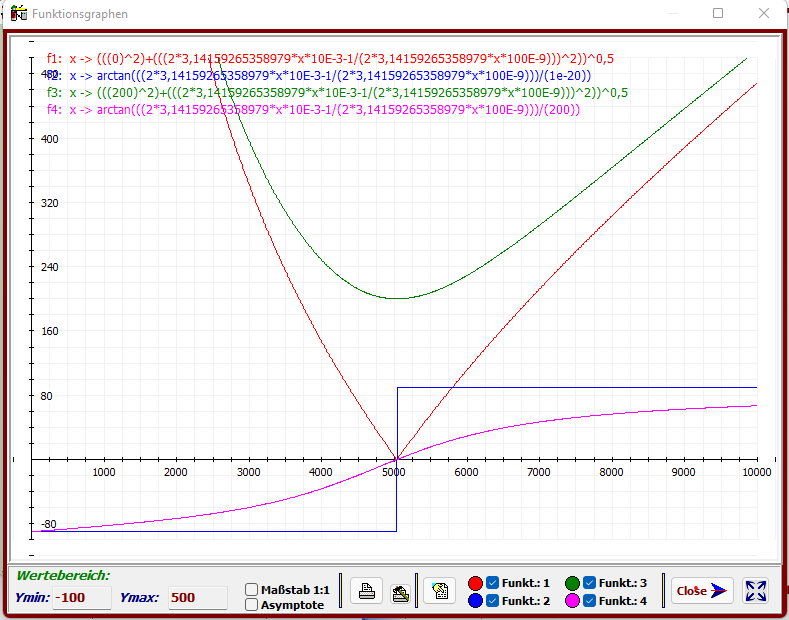
Verwendete Werte: R = 200 Ω → R = 200, X
L
: L= 10 mH (10e-3 H ) → L = 10e-3;
Winkelmodus: Gradmaß (360°)
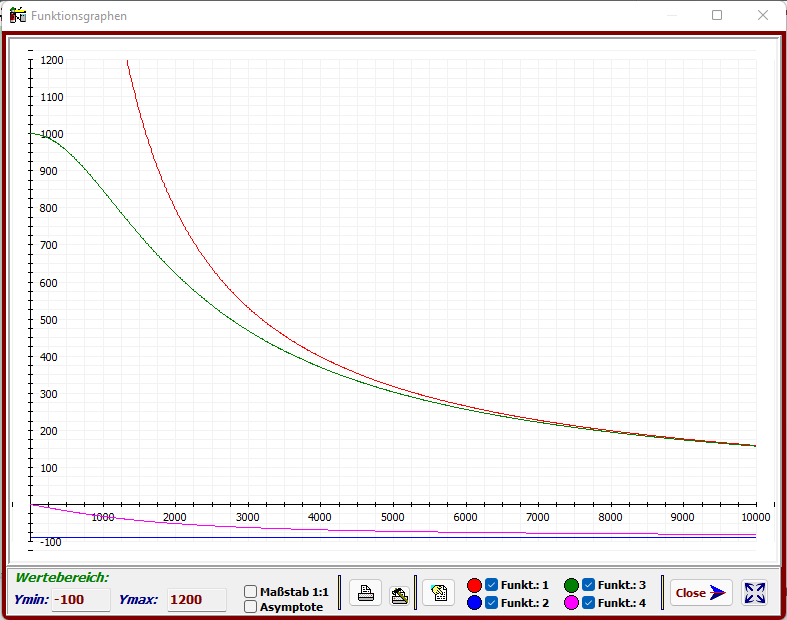
Der Einfluss des ohmschen Spulenwiderstandes (grün, magenta) ist deutlich erkennbar.
Im Gegensatz zur idealen Spule (rot, R=0) verläuft die Widerstandskurve bei der realen Spule (R>0)
speziell im unteren Frequenzbereich nicht linear. Sie nähert sich asymptotisch der Widerstands-
geraden der idealen Spule. Dieses Verhalten ist auch dem Phasengang zu entnehmen.
Kapazitive Widerstände können in vielen Fällen vereinfacht als Parallelschaltung eines idealen
Kondensators und einem ohmschen Widerstand dargestellt werden.
R
C
= Ohmscher Widerstand (Leckwiderstand usw.)
X
C
= Kapazitiver Widerstand (Blindwiderstand)
Ideale Kondensatoren besitzen nur den Blindwiderstand X
C
(der parallele Widerstand ist unendlich
groß; R
c
→ ∞). Der Realteil ist gleich 0.
Variable x = f, Parameter C = C [F]
Real- und Imaginärteile (grau) eingesetzt in die Formelgerüste für Z und φ führt zu den direkt durch
kopieren einsetzbaren Funktionen (Formeln):
f
1
: |Z(x)| = {[( 0 )^2] + [( -1 / (2*Pi*x*C) )^2]}^0,5
f
2
: φ(x) = - 90° (reiner kapazitiver Widerstand; Realteil ist 0)
Reale Kondensatoren besitzen besonders in der Hochfrequentechnik zusätzlich zum eigentlichen
kapazitiven Widerstand weiter Einflussgrößen, siehe Beispiel oben.
Im Normalfall reicht es aus, die ohmschen Widerstände als Parallelwiderstand R
C
zusammen zu
fassen.
Für Parallelschaltungen gilt: Y
ges
= Y
1
+ Y
2
+ Y
3
+ … + Y
n
und als Ergebnis:
Empfehlung: Der Übersicht halber sollten R als Spulenreihen- und W als Kondensatoparallel-
widerstand verwendet werden.
Variable x = f, Parameter W = R [Ω]; C = C [F]
Real- und Imaginärteile eingesetzt in die Formelgerüste für Z und φ. Dieses führt zu direkt
kopierbaren und in den Kleinen Rechner einsetzbaren Funktionen (Formeln):
f
3
: |Z(x)| = {[( W / ( 1 + (W*C*2*Pi*X)^2) )^2] + [( { - (W^2*C*2*Pi*X ) / ( 1 + (W*C*2*Pi*X)^2) } )^2]}^0,5
f
4
: φ(x) = arctan[ ( { - (W^2*C*2*Pi*X ) / ( 1 + (W*C*2*Pi*X)^2) } ) / ( W / ( 1 + (W*C*2*Pi*X)^2) ) ]
Verwendete Werte: R
C
= 1000 Ω → W=1000; X
C
: C = 100 nF (100E-9 F ) → C = 100E-9;
Winkelmodus: „Gradmaß (360°)“ !
Der Einfluss des ohmschen Verlustwiderstandes (grün, Magenta) ist auch hier deutlich erkennbar.
Der parallele Widerstand R
C
begrenzt den maximalen Widerstand Z
C
des Kondensators.
In den Formeln verwendete Parameter: W, C, R, L
Verwendete Werte: R
C
= 1000 Ω → Parameter W = 1000; X
C
: C = 100 nF (100E-9 F )
→ C = 100E-9 ,
R
L
= 200 Ω → Parameter R = 200; X
L
: L = 10 mH (10e-3 H ) → L = 10E-3 ;
Verwendete Formeln: siehe oben
Indeale Spule:
f
1
: |Z(x)| = {[( 0 )^2] + [( 2*Pi*x*L )^2]}^0,5
Reale Spule:
f
2
: |Z(x)| = {[( R )^2] + [( 2*Pi*x*L )^2]}^0,5
Idealer Kondensator:
f
3
: |Z(x)| = {[( 0 )^2] + [( -1 / (2*Pi*x*C) )^2]}^0,5
Realer Kondensator:
f
4
: |Z(x)| = {[( W / ( 1 + (W*C*2*Pi*X)^2) )^2] + [( { - (W^2*C*2*Pi*X ) / ( 1 + (W*C*2*Pi*X)^2) } )^2]}^0,5
Bitte beachten Sie, dass die Kurven die jeweiligen Scheinwiderstände |Z
L
(f)| und |Z
C
(f)| abbilden.
Nur die rote und grüne Kurven repräsentieren die Bildwiderstände |X
L
| und |X
C
|.

Verlustfreie und verlustbehaftete Kondensatoren:
Verlustfreie und verlustbehaftete Kondensatoren:
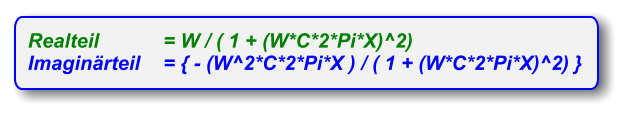


Verlustfreie und verlustbehaftete Spule:
Verlustfreie und verlustbehaftete Spule:







C
R
ESR
L
ESL
R
isol
, R
leak


R
L
X
L
Ideale (verlustfreie) Spulen:
Ideale (verlustfreie) Spulen:
Reale (verlustbehaftete) Spulen:
Reale (verlustbehaftete) Spulen:

Z
L
= jX
L
↔ Z
L
= j
ωL ↔ Z
L
= j
2πf L

Z
L
= R
L
+ jX
L
↔ Z
L
= R
L
+ j
ωL ↔ Z
L
= R
L
+ j
2πf L
Ideale (verlustfreie) Kondensatoren:
Ideale (verlustfreie) Kondensatoren:
R
C
X
C
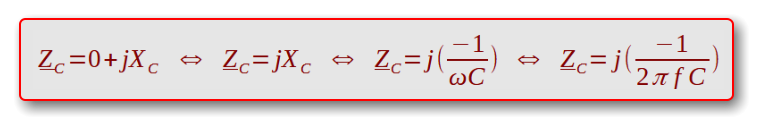
Reale (verlustbehaftete) Kondensatoren:
Reale (verlustbehaftete) Kondensatoren:

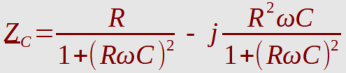

Gegenüberstellung: Spule und Kondesator:
Gegenüberstellung: Spule und Kondesator:
Formelumsetzung - Erstellung
Formelumsetzung - Erstellung
Formelumsetzung - Erstellung
Formelumsetzung - Erstellung
Formelumsetzung - Erstellung
Formelumsetzung - Erstellung
Formelumsetzung - Erstellung
Formelumsetzung - Erstellung


X
C

R
C
X
C

R
L
X
L

X
C
Anmerkung: Alle Verlustwiderstände der Spule sind in R
L
subsumiert.
R
L
= Ohmscher Widerstand der Wicklungen usw.
X
L
= Induktiver Widerstand (Blindwiderstand)
X
C
= Kapazitiver Widerstand (Blindwiderstand)
Im verlustfreien Reihenschwingkreis ist der Widerstand R
L
= 0
Variable x = f, Parameter L = L [H]; C = C [F]
f
1
: |Z(x)| = {[( 0 )^2] + [( { 2*Pi*x*L - 1/(2*Pi*x*C) } )^2]}^0,5
f
2
: φ(x) = arctan[ ( { 2*Pi*x*L - 1/(2*Pi*x*C) } ) / ( 1e-20 ) ] (mit Realteil ≠ 0)
(da der Wert eines potentiellen Widerstandes immer ≥ 0 ist, reicht hier der Wert 1e-20 ≈ 0 (x
0r
- für rechtsseitigen Grenzwert) aus.)
Im verlustbehafteten Reihenschwingkreis ist der Widerstand R
L
> 0
Variable x = f, Parameter R = R
L
[Ω]; L = L [H]; C = C [F]
f
3
: |Z(x)| = {[( R )^2] + [( { 2*Pi*x*L - 1/(2*Pi*x*C) } )^2]}^0,5
f
4
: φ(x) = arctan[ ( { 2*Pi*x*L - 1/(2*Pi*x*C) } ) / ( R ) ] (mit Realteil ≠ 0)
In den Formeln verwendete Parameter: C, R, L
Werte: R
gm
= 200 Ω (grün, magenta) → R=200; X
L
: L = 10 mH → L=10E-3; X
C
: C = 100 nF → C = 100e-9;
Winkelmodus: Gradmaß (360°)
Der Einfluss des ohmschen Verlustwiderstandes (grün, magenta) ist auch hier deutlich erkennbar.
Der minimale Widerstand wird hier durch R
L
begrenzt.

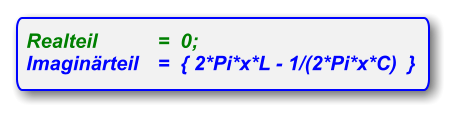
Formelumsetzung - Erstellung
Formelumsetzung - Erstellung
Realer (verlustbehafteter) Reihenschwingkreis:
Realer (verlustbehafteter) Reihenschwingkreis:
Idealer (verlustfreier) Reihenschwingkreis:
Idealer (verlustfreier) Reihenschwingkreis:




Formelumsetzung - Erstellung
Formelumsetzung - Erstellung

R
L
X
L

X
C
X
L


X
C
Anmerkung: Alle Verlustwiderstände sind in R
V
subsumiert.
R
V
= Ohmscher Widerstand (enthält alle ohmschen Verluste)
X
L
= Induktiver Widerstand (Blindwiderstand)
X
C
= Kapazitiver Widerstand (Blindwiderstand)
Im verlustfreien Parallelschwingkreis fehlt der Widerstand R
V
bzw. strebt er gegen Unendlich.
Variable x = f, Parameter L = L [H]; C = C [F]
f
1
: |Z(x)| = {[( 0 )^2] + [( { 2*Pi*x*L / ( 1 - (2*Pi*x)^2 *L*C) } )^2]}^0,5
f
2
: φ(x) = arctan[ ( { 2*Pi*x*L / ( 1 - (2*Pi*x)^2 *L*C) } ) / ( 1e-20 ) ] (mit Re ≠ 0; Division durch 0 -> 1e-20 ≈ 0)
(da der Wert eines potentiellen Widerstandes immer ≥ 0 ist, reicht hier der Wert 1e-20 ≈ 0 (x
r
- für rechtsseitigen Grenzwert) aus.)
Im verlustbehafteten Parallelschwingkreis ist der Widerstand (Leckwiderstand usw.) R
V
> 0.
Variable x = f, Parameter W = R
V
[Ω]; L = L [H]; C = C [F]
f
3
: |Z(x)| = {[( { [ 1 / W ] / [ 1/W^2 + { 2*Pi*x*C - 1/(2*Pi*x*L) }^2 ] } )^2] + [( { [ 1 / (2*Pi*x*L) - 2*Pi*x*C ]
/ [ 1/W^2 + { 2*Pi*x*C - 1/(2*Pi*x*L) }^2 ] } )^2]}^0,5
f
4
: φ(x) = arctan[ ( { [ 1 / (2*
Pi*x*L) - 2*Pi*x*C ] / [ 1/W^2 + { 2*Pi*x*C - 1/(2*Pi*x*L) }^2 ] } ) / ( { [ 1 / W ]
/ [ 1/W^2 + { 2*Pi*x*C - 1/(2*Pi*x*L) }^2 ] } ) ] (mit Re ≠ 0; Winkeleinstellung: Altgrad 360°)
Verwendete Parameter: W, L, C
Werte: R
V
= 1000 Ω → W = 1000; X
L
: L= 10 mH (10e-3 H ) → L = 10e-3; X
C
: C = 100 nF (100e-9 F) → C = 100e-9;


![Realteil = { [ 1 / W ] / [ 1/W^2 + { 2*Pi*x*C - 1/(2*Pi*x*L) }^2 ] } Imaginärteil = { [ 1 / (2*Pi*x*L) - 2*Pi*x*C ] / [ 1/W^2 + { 2*Pi*x*C - 1/(2*Pi*x*L) }^2 ] }](index_htm_files/130939.png)

Komplexer Leitwert:
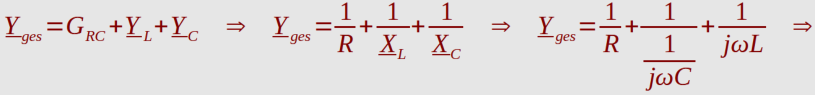
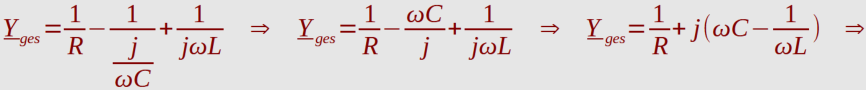
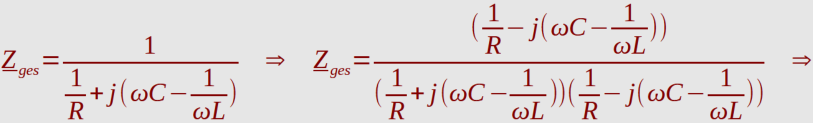
Widerstand Z
ges
konjugiert komplex erweitert
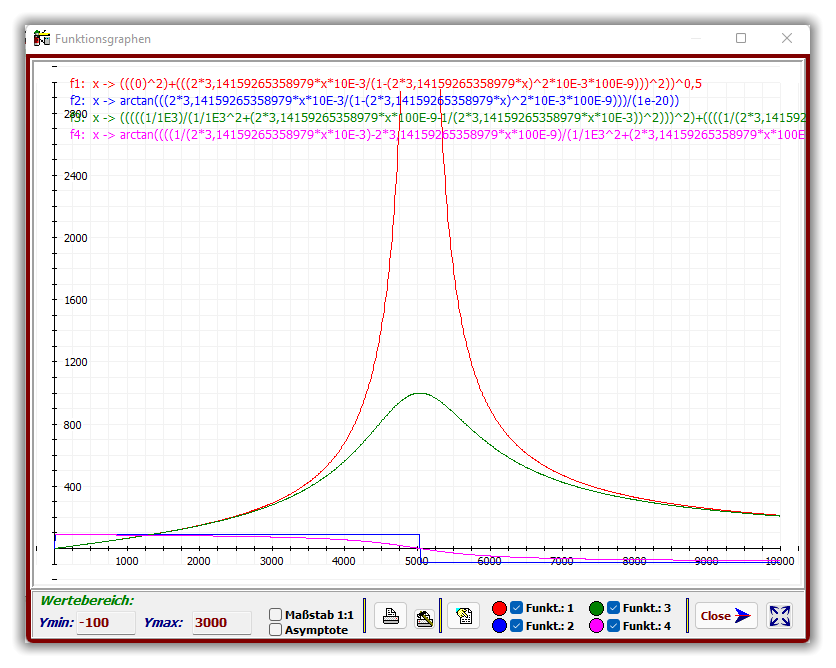
Idealer (verlustfreier) Parallelschwingkreis:
Idealer (verlustfreier) Parallelschwingkreis:
Formelumsetzung - Erstellung
Formelumsetzung - Erstellung


X
L
X
C


Realer (verlustbehafteter) Parallelschwingkreis:
Realer (verlustbehafteter) Parallelschwingkreis:

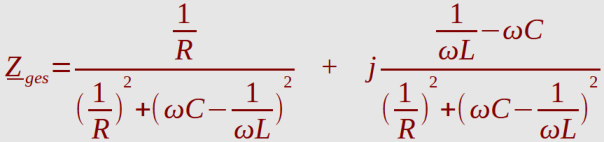
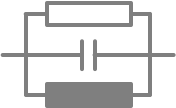
X
L
R
V
X
C
Formelumsetzung - Erstellung
Formelumsetzung - Erstellung


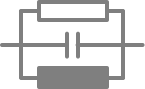
X
L
R
V
X
C
Variable x = f, Parameter R = R
L
[Ω]; L = L [H]; C = C [F]
f
1
: |Z(x)| = {[( R )^2] + [( { 2*Pi*x*L - 1/(2*Pi*x*C) } )^2]}^0,5
f
2
: φ(x) = arctan[ ( { 2*Pi*x*L - 1/(2*Pi*x*C) } ) / ( R ) ] (mit Realteil ≠ 0)
Variable x = f, Parameter W = R
V
[Ω]; L = L [H]; C = C [F]
f
3
: |Z(x)| = {[( { [ 1 / W ] / [ 1/W^2 + { 2*Pi*x*C - 1/(2*Pi*x*L) }^2 ] } )^2] +
[( { [ 1 / (2*Pi*x*L) - 2*Pi*x*C ] / [ 1/W^2 + { 2*Pi*x*C - 1/(2*Pi*x*L) }^2 ] } )^2]}^0,5
f
4
: φ(x) = arctan[ ( { [ 1 / (2*Pi*x*L) - 2*Pi*x*C ] / [ 1/W^2 + { 2*Pi*x*C - 1/(2*Pi*x*L) }^2 ] } ) /
( { [ 1 / W ] / [ 1/W^2 + { 2*Pi*x*C - 1/(2*Pi*x*L) }^2 ] } ) ]
Verwendete Parameter: Spule: R, L; Kondensator: W, C; Winkelmodus: „Gradmaß (360°)“
Werte: X
L
: L = 10 mH → L = 10E-3; R
L
= 50 Ω → R = 50; X
C
: C = 100 nF → C = 100e-9; R
V
= 1000 Ω → W = 1000;
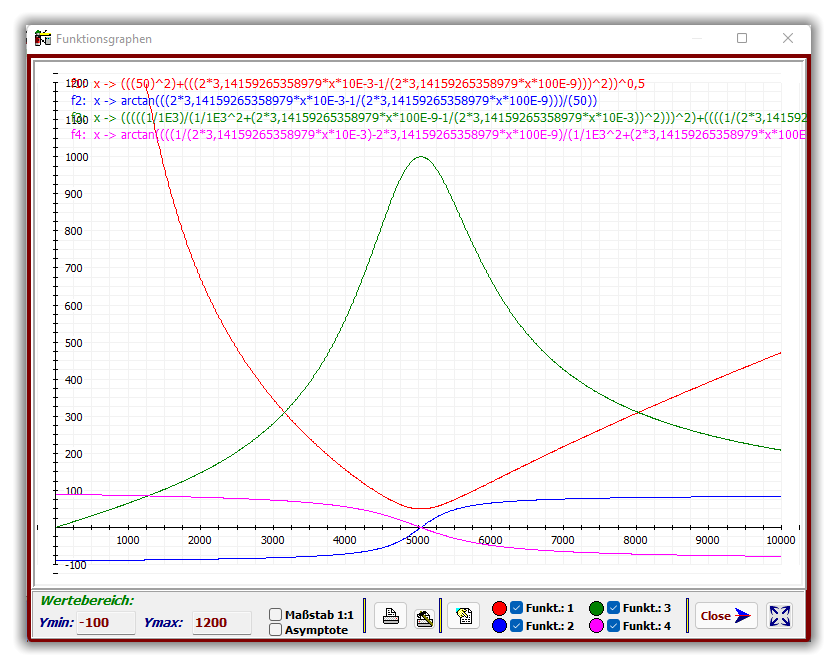
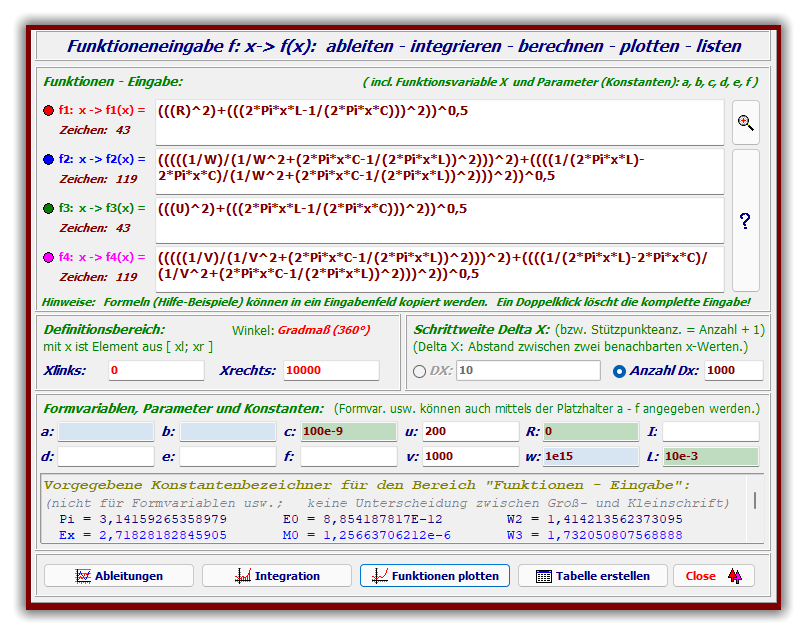
Zur zusammenhängenden Übersicht werden vier Funktionsgleichungen aus den oben dargestell-
ten Formeln für ideale und reale Schwingkreise mit Hilfe von Widerstandsparametern als Modi-
fikationen erstellt.
Reihenschwingkreis f
1
und f
3
:
f
1
: |Z
Reihe_1
(X)| = { [ ( R )^2 ] + [ ( { 2*Pi*x*L - 1/(2*Pi*x*C) } )^2 ] }^0,5
f
3
: |Z
Reihe_3
(X)| = { [ ( U )^2 ] + [ ( { 2*Pi*x*L - 1/(2*Pi*x*C) } )^2 ] }^0,5
Parallelschwingkreis f
2 und
f
4
:
f
2
: |Z
Parallel_2
(X)| = { [ ( { [ 1 / W ] / [ 1/W^2 + { 2*Pi*x*C - 1/(2*Pi*x*L) }^2 ] } )^2 ] + [ ( { [ 1 / (2*Pi*x*L) - 2*Pi*x*C ] /
[ 1/W^2 + { 2*Pi*x*C - 1/(2*Pi*x*L) }^2 ] } )^2 ] }^0,5
f
4
: |Z
Parallel_4
(X)| = { [ ( { [ 1 / V ] / [ 1/V^2 + { 2*Pi*x*C - 1/(2*Pi*x*L) }^2 ] } )^2 ] + [ ( { [ 1 / (2*Pi*x*L) - 2*Pi*x*C ] /
[ 1/V^2 + { 2*Pi*x*C - 1/(2*Pi*x*L) }^2 ] } )^2 ] }^0,5
_______________
Werte für ideale Schwingkreise (f
1
u. f
2
):
R
L
= 0 Ω
→ R = 0;
X
L
: L = 10 mH → L= 10E-3;
R
V
ist sehr groß
→ W = 1E15;
X
C
: C = 100 nF → C= 100E-9;
Werte für reale Schwingkreise (f
3
u. f
4
):
R
L
= 200 Ω
→ U = 200;
X
L
: L= 10 mH → L= 10E-3;
R
V
= 1 kΩ
→ V = 1000;
X
C
: C = 100 nF → C= 100E-9;
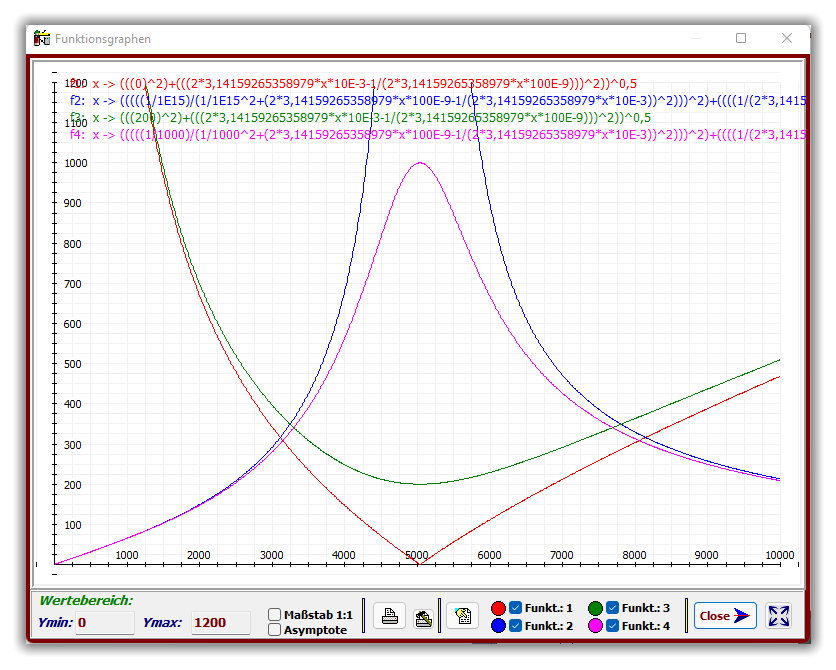
Durch die Werte R=0 (Reihenschwingkreis) und W=1e15 (Parallelschwingkreis, W≠0; 1e15 ist
ausreichend groß) werden ideale Schwingkreise simuliert.
Im Resonanzbereich (ca. 5033 Hz) ist der ideale Reihenschwingkreis widerstandslos. Als realer
Schwingkreis (grün) wird hier sein Gesamtwiderstand nur durch den ohmschen Widerstand
repräsentiert (R=200 Ω) (Saugkreis).
Der ideale Parallelschwingkreis zeigt im Resonanzfall einen gegen Unendlich strebenden
Gesamtwiderstand. Als realer Schwingkreis wird hier der maximale Widerstand durch den
ohmschen Parallelwiderstand begrenzt (Sperrkreis).
Realer (verlustbehafteter) Parallelschwingkreis:
Realer (verlustbehafteter) Parallelschwingkreis:

X
L
R
V
X
C
Reale Schwingkreise: Gegenüberstellungen
Reale Schwingkreise: Gegenüberstellungen

Realer (verlustbehafteter) Reihenschwingkreis:
Realer (verlustbehafteter) Reihenschwingkreis:
R
L
X
L

X
C


Ideale und reale Schwingkreise: Gegenüberstellungen
Ideale und reale Schwingkreise: Gegenüberstellungen
R
L
X
L

X
C

X
L
R
V
X
C
Von Spannungsüberhöhungen spricht man, wenn im Reihenschwingkreis die Blindspannungen U
C
und U
L
höher sind als die Eingangsspannung U
e
. Diese an sich gefährliche Eigenschaft kann auch
erwünscht sein, zum Beispiel um in batteriebetriebenen Schaltungen wesentlich höhere
Spannungen abgreifen zu können.
Anmerkung: Die real existierenden Spannungen U
C
und U
L
sind gegenseitig um 180° phasen-
verschoben. In der Summe heben sie sich folglich gegenseitig auf.
Da im Resonanzfall die komplexen Widerstände sich gegensätzlich aufheben, wird der Stom nur
noch durch den ohmschen Widerstand begrenzt. Die an den komplexen Widerständen X
C
und X
L
abfallenden Spannungen haben dann den höchsten Wert.
Auch im komplexen Bereich gilt das 2. Kirchhoffsches Gesetz (Maschenregel) ∑ U = 0
Exemplarisch wird hier der Spannungsverlauf U
L
an der Spule in Abhängigkeit der Frequenz
ermittelt.
In einer Reihenschaltung ist der fließende Strom in allen
Widerständen gleich.
Formel in Real- und Imaginärteil splitten:
Variable x = f (ω = 2ℼf), Parameter L = L [H]; C = C [F]; R = R [Ω]
Nenner
= [ { 1-1/[ (2*Pi*x)^2*C*L ] }^2 + { R/[2*Pi*x*L] }^2 ]
Re(Zähler)
= [ 1-1/[(2*Pi*x)^2*C*L] ]
Im(Zähler)
= [ R/(2*Pi*x*L) ]
f
1
: |Z(x)| = {[( [ 1-1/[(2*Pi*x)^2*C*L] ] / [ { 1-1/[ (2*Pi*x)^2*C*L ] }^2 + { R/[2*Pi*x*L] }^2 ] )^2] +
[( [ R/(2*Pi*x*L) ] / [ { 1-1/[ (2*Pi*x)^2*C*L ] }^2 + { R/[2*Pi*x*L] }^2 ] )^2]}^0,5
φ(x) = arctan[ ( [ R/(2*Pi*x*L) ] / [ { 1-1/[ (2*Pi*x)^2*C*L ] }^2 + { R/[2*Pi*x*L] }^2 ] ) /
( [ 1-1/[(2*Pi*x)^2*C*L] ] / [ { 1-1/[ (2*Pi*x)^2*C*L ] }^2 + { R/[2*Pi*x*L] }^2 ] ) ]
Der Spannungüberhöhungsfaktor ist vom Widerstand R abhängig. Zum Vergleich sollen hier noch
drei weitere Kurven mit unterschiedlichen Widerstandswerten dargestellt werden. Hierfür werden
für R die weiteren Parameter U, V und W verwendet.
Empfehlung:
- Kopieren Sie die Terme f
1
bis f
4
in das jeweilige Eingabefeld,
- löschen Sie alle Parameter (Doppelcklick auf Mülltonne),
- starten Sie die Plotausgabe (Funktionen plotten) und
- verlassen Sie anschließend das Plotfenster (Esc-Taste).
Als Ergebnis werden die noch nicht festgelegten Parameter angezeigt (????)!
f
2
: Z(x)| = {[( [ 1-1/[(2*Pi*x)^2*C*L] ] / [ { 1-1/[ (2*Pi*x)^2*C*L ] }^2 + { U/[2*Pi*x*L] }^2 ] )^2] +
[( [ U/(2*Pi*x*L) ] / [ { 1-1/[ (2*Pi*x)^2*C*L ] }^2 + { U/[2*Pi*x*L] }^2 ] )^2]}^0,5
f
3
: |Z(x)| = {[( [ 1-1/[(2*Pi*x)^2*C*L] ] / [ { 1-1/[ (2*Pi*x)^2*C*L ] }^2 + { V/[2*Pi*x*L] }^2 ] )^2] +
[( [ V/(2*Pi*x*L) ] / [ { 1-1/[ (2*Pi*x)^2*C*L ] }^2 + { V/[2*Pi*x*L] }^2 ] )^2]}^0,5
f
4
: |Z(x)| = {[( [ 1-1/[(2*Pi*x)^2*C*L] ] / [ { 1-1/[ (2*Pi*x)^2*C*L ] }^2 + { W/[2*Pi*x*L] }^2 ] )^2] +
[( [ W/(2*Pi*x*L) ] / [ { 1-1/[ (2*Pi*x)^2*C*L ] }^2 + { W/[2*Pi*x*L] }^2 ] )^2]}^0,5
Verwendete Werte:
X
L
: L = 10 mH (10e-3 H ); X
C
: C = 100 nF (100e-9 F);
Parameter R
1
- R
4
:
R
1
= 0,5 Ω (rot);
R
2
= 1 Ω (blau);
R
3
= 2 Ω (grün);
R
4
= 5 Ω (magenta)
also:
R = 0,5;
U = 1;
V = 2;
W = 5
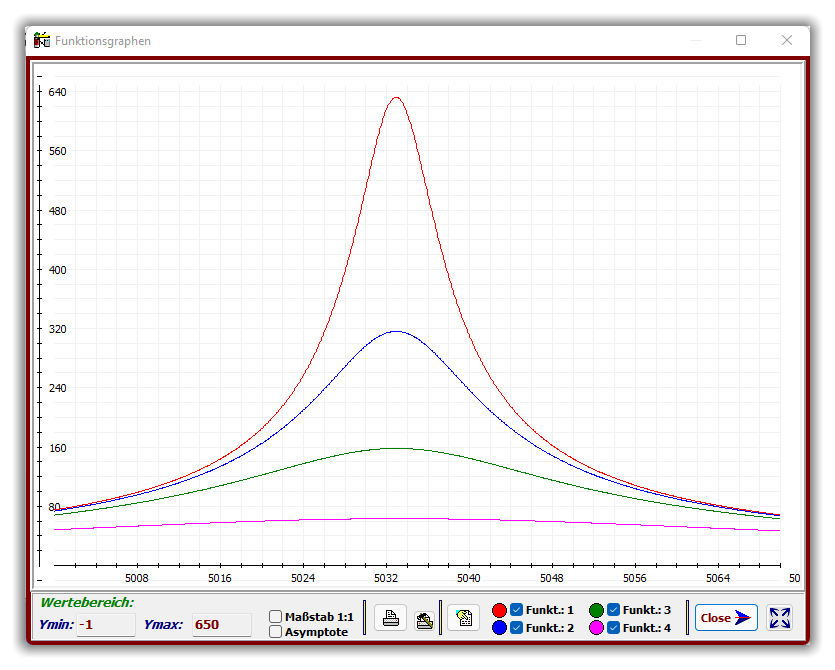
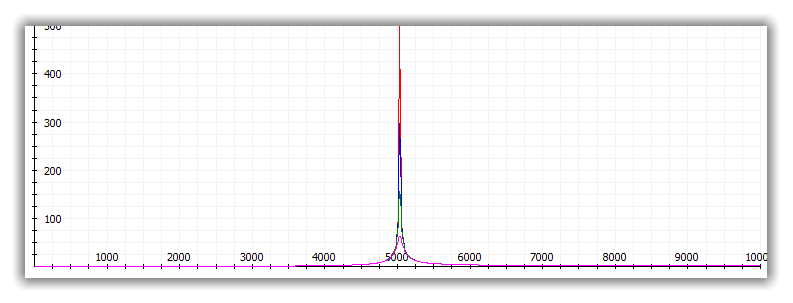
Die Spannungswerte an der Spule sind bis ca. 4,5 kHz unauffällig, ändern sich dann aber extrem.
Wie die rote Kurve zeigt, liegen im Resonanzfall an der Spule (und um 180° verschoben ebenfalls
am Kondensator) mehr als die 600-fache Eingangspannung an, vorausgesetzt, dass die
Spannungsquelle den hierfür notwendigen Strom liefern kann (Gesamtwiderstand dieses Reihen-
schwingkreises im Resonanzfall = 0,5 Ω).
Hinweis: Siehe hierzu auch den nachfolgenden Abschnitt „Beispiel: Tief- und Hochpass“
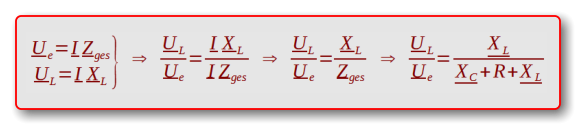

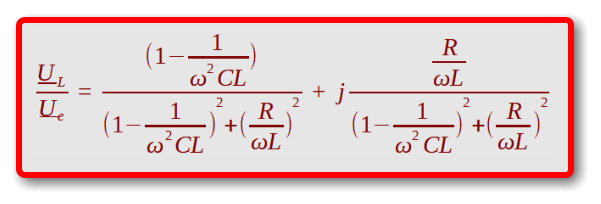
Formelumsetzungen für Plotausgaben
Formelumsetzungen für Plotausgaben
Realer (verlustbehafteter) Reihenschwingkreis:
Realer (verlustbehafteter) Reihenschwingkreis:
Spannungsverhältnisse im Reihenschwingkreis:
Spannungsverhältnisse im Reihenschwingkreis:

Realteil
= [ 1-1/[(2*Pi*x)^2*C*L] ] / [ { 1-1/[ (2*Pi*x)^2*C*L ] }^2 + { R/[2*Pi*x*L] }^2 ]
Imaginärteil
= [ R/(2*Pi*x*L) ] / [ { 1-1/[ (2*Pi*x)^2*C*L ] }^2 + { R/[2*Pi*x*L] }^2 ]

Spannungsüberhöhungen:
Spannungsüberhöhungen:
Ansatz:
Ansatz:
Formelerstellung:
Formelerstellung:

U
C
+ U
R
+ U
L
- U
e
= 0 ⇒ U
e
= U
C
+ U
R
+ U
L
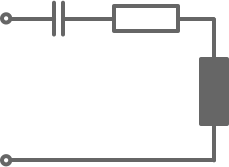




U
C
U
L
U
R
U
e
X
C
X
L
R


I
Berechnungen:
Berechnungen:
Übersicht - Frequenzbereich von 0 - 10 kHz:
Übersicht - Frequenzbereich von 0 - 10 kHz:
Teildarstellung - Frequenzbereich von 5000 - 5070 Hz:
Teildarstellung - Frequenzbereich von 5000 - 5070 Hz:























