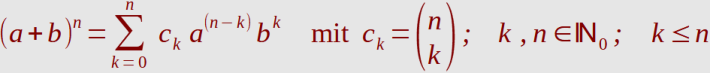Dieser Rechner für Funktionen ermöglicht es unter anderem,
a. Wertetabellen zu erstellen,
b. Funktionsgraphen zu plotten,
c. Riemannsche Summen zu plotten bzw. bestimmte Integrale zu berechnen,
d. Funktionsgraphen und die zugehörigen ersten drei Ableitungen grafisch
auszugeben,
e. Listen zu generieren usw.
Alle angeführten Beispiele können durch Kopieren und Einfügen (copy and paste) direkt im
Bereich „Funktioneneingabe“ in die Eingabefelder f
1
bis f
4
übernommen werden.
Die hier zu sehenden Screenshots der Plotausgaben sind zur besseren Wiedergabe (Skalierung
der Screenshots) bewusst nicht im Modus „Vollbildschirm“ erstellt worden.
Eine zusätzliche Druckausgabe der Ergebnisse ist immer möglich.
(Hinweis: Die Pfeile dienen auch als Links!)
1. Binomialkoeffizienten:
Koeffizienten eines Binoms vom Grade n berechnen und als Liste ausgeben.
2. Beispiel Stochastik:
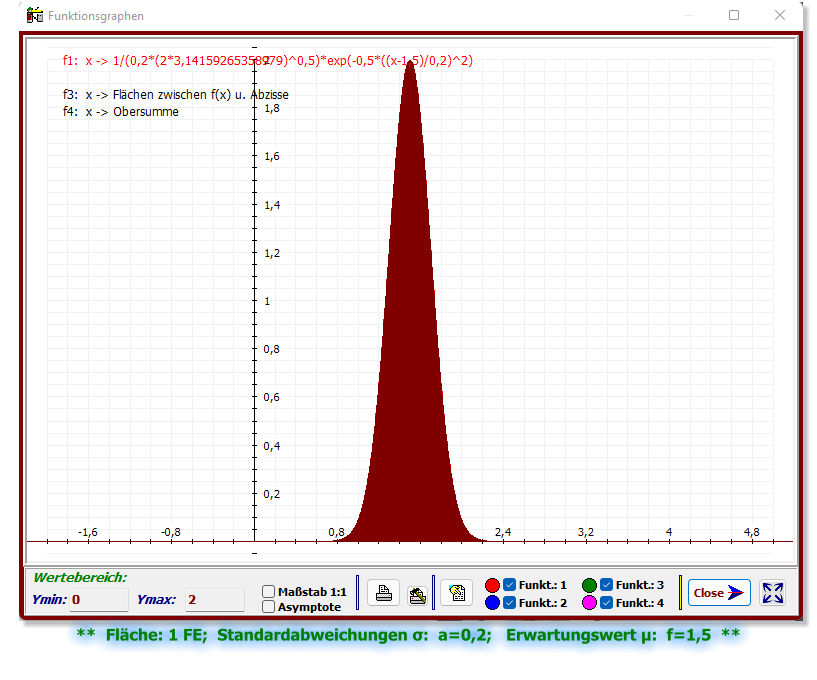
Experimentieren mit unterschiedlichen Dichtefunktionen - Glockenkurven.
3. Beispiel Stochastik:
Experimentieren mit der Integration (uneigentliche Integrale) unterschiedlicher
Dichtefunktionen - Glockenkurven.
4. Beispiel Stochastik:
Exemplarische Berechnungen mittels Integration einiger Tabellenwerte für
Standardnormalverteilungen.
Exemplarische Beispiele:
Exemplarische Beispiele:




Standardnormalverteilung oder normierten Normalverteilung
Standardnormalverteilung oder normierten Normalverteilung

Beispiel für Normalverteilung: Dichtefunktion - Verteilungsfunktion
Die Normalverteilung (Gauß-Verteilung) wird auch „Gaußsche Glockenkurve“ genannt, da der
Kurvenverlauf der Dichtefunktion auch als Glockenform zu deuten ist.
Die Dichtefunktion ist in zwei Darstellungsformen gebräuchlich. Diese unterscheiden sich, wie
erkennbar ist, lediglich durch einfache Umformungen.
Erwartungswert μ; Varianz σ²; Standardabweichung σ
Denken Sie daran, dass vom Programm interpretierbare Terme alle Operatoren enthalten müssen.
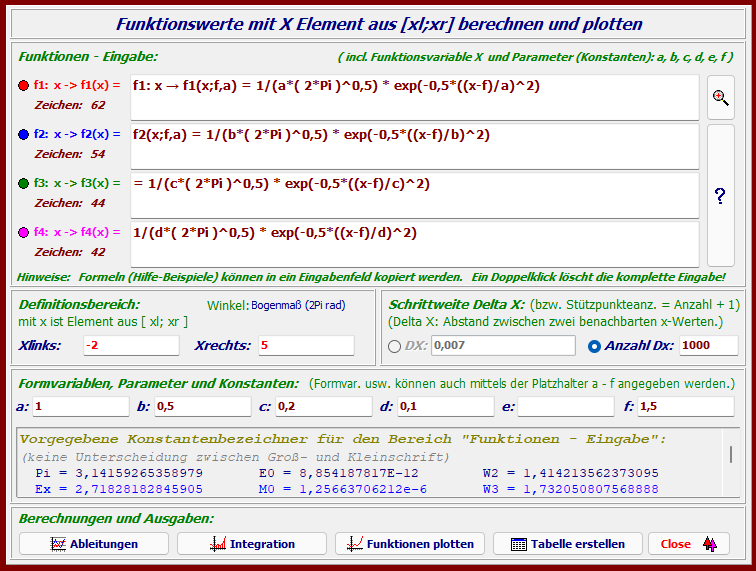
Empfehlung: Um mit der Dichtefunktion einfach experimentieren zu können, sollten der
Erwartungswert μ und die Standardabweichung σ im Programm durch zugelassene
Konstanten ersetzt werden. Diese Werte können dann sehr schnell durch neue
Eingaben (Überschreibung) verändert werden.
Mit dem Erwartungswert μ, ersetzt durch f sowie der Standardabweichung σ, ersetzt durch jeweils
a, b, c und d, folgen für die Dichtefunktionen als vom Programm akzeptierte kopierbare Formel:
f
1
: x → f
1
(x;μ,σ):
f
1
: x → f
1
(x;f,a) = 1/(a*( 2*Pi )^0,5) * exp(-0,5*((x-f)/a)^2)
f
2
: x → f
2
(x;μ,σ):
f
2
: x → f
2
(x;f,b) = 1/(b*( 2*Pi )^0,5) * exp(-0,5*((x-f)/b)^2)
f
3
: x → f
3
(x;μ,σ):
f
3
: x → f
3
(x;f,c) = 1/(c*( 2*Pi )^0,5) * exp(-0,5*((x-f)/c)^2)
f
4
: x → f
4
(x;μ,σ):
f
4
: x → f
4
(x;f,d) = 1/(d*( 2*Pi )^0,5) * exp(-0,5*((x-f)/d)^2)
Diese können dann für f
1
bis f
4
einzeln kopiert und eingegeben werden. Alle normalen Zeichen
links vom Gleichheitszeichen sowie das Gleichheitszeichen selbst werden ignoriert.
Für den Definitionsbereich werden die Werte xl = -2 und xr = 5 als Erstwerte empfohlen.
Standardabweichungen σ: a=1; b=0,5; c=0,2; d=0,1; (Entertaste) Erwartungswert μ: f=1,5


Beispiel Stochastik:
Beispiel Stochastik:



Anwendungsbereich: Normalverteilung:
Anwendungsbereich: Normalverteilung:

Die Dichtefunktion:
Die Dichtefunktion:





Anwendungsbereich: Normalverteilung:
Anwendungsbereich: Normalverteilung:

Die Verteilungsfunktion:
Die Verteilungsfunktion:
Durch Integration der Dichtefunktion erhält man die Verteilungsfunktion.
Die Verteilungsfunktion F(x) gibt an, wie groß die Wahrscheinlichkeit ist, dass die (stetige) Zufalls-
variable X einen Wert annimmt, der kleiner oder gleich x ist, also F(x) = P( X ≤ x )
Für das Integral in den Grenzen x
1
→ -∞ und x
2
→ ∞ gilt: F(x) = 1
Unter der Voraussetzung, dass die obigen Dichtefunktionen bereits eingegeben (und
sinnvollerweise zur Übersicht auch einmal gezeichnet worden) sind,
f
1
: x → f
1
(x;μ,σ):
f
1
: x → f
1
(x;f,a) = 1/(a*( 2*Pi )^0,5) * exp(-0,5*((x-f)/a)^2)
f
2
: x → f
2
(x;μ,σ):
f
2
: x → f
2
(x;f,b) = 1/(b*( 2*Pi )^0,5) * exp(-0,5*((x-f)/b)^2)
f
3
: x → f
3
(x;μ,σ):
f
3
: x → f
3
(x;f,c) = 1/(c*( 2*Pi )^0,5) * exp(-0,5*((x-f)/c)^2)
f
4
: x → f
4
(x;μ,σ):
f
4
: x → f
4
(x;f,d) = 1/(d*( 2*Pi )^0,5) * exp(-0,5*((x-f)/d)^2)
(Standardabweichungen σ: a=1; b=0,5; c=0,2; d=0,1; Erwartungswert μ: f=1,5)
können im Programmabschnitt „Integration“ die Werte, insbesondere für die
Grenzen x
1
→ -∞ und x
2
→ ∞, näherungsweise berechnet werden.
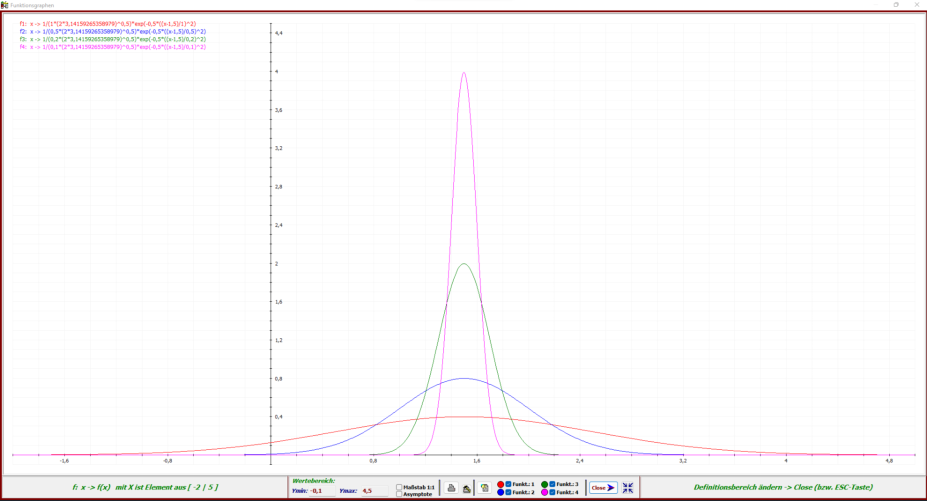
Hinsichtlich der Verlaufsformen der obigen Glockenkurven erhält man bereits mit den
Integrationsgrenzen x
1
= -4 und x
2
= 6 sowie der Schrittanzahl von 1000 sehr gute
Näherungswerte.
1.
Die zu integrierenden Beispielfunktionen f
1
,..,f
4
befinden sich in den jeweiligen
Eingabefenstern.
2.
Zum Bereich Integration wechseln (Button).
3.
Den Definitionsbereich x
a
= -5 und x
b
= 7 eingeben. Dieser dient hier lediglich zur Festle-
gung der Ansichtsgrenzen im Ausgabebereich. Auf die Integration hat er keinen Einfluss.
4.
Die Integrationsgrenzen (Integrationsintervall) x
a
= -4 und x
b
= 6 eingeben.
Die Genauigkeit ist abhängig von der Schrittweite.
5.
Im Bereich „Zuordnung(en)“ f: Funktion Nr.: 1 wählen.
6.
Berechnen und anschließend zeichnen lassen (Buttons)
7.
Restliche Funktionen (2, 3 und 4) wählen, berechnen und zeichnen lassen.
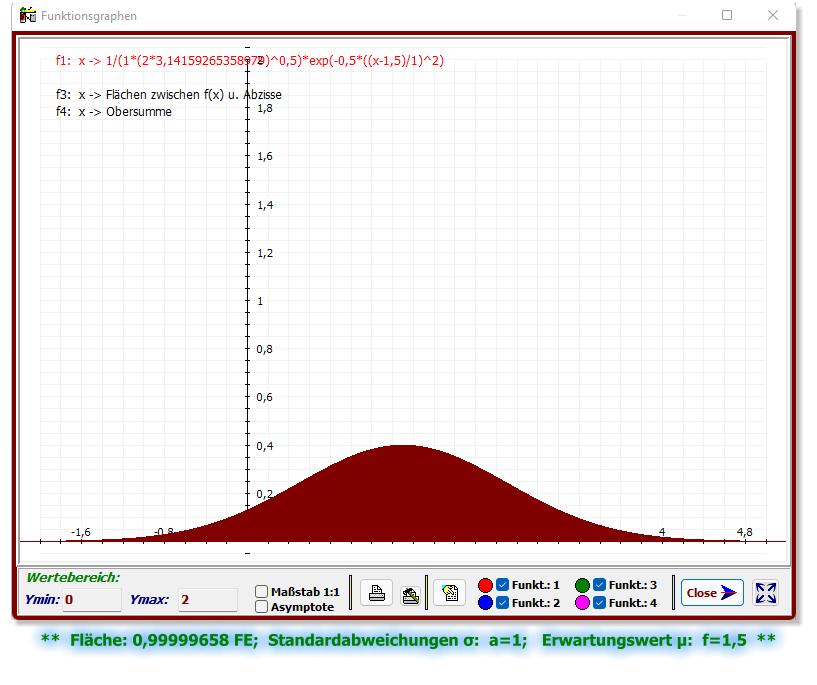
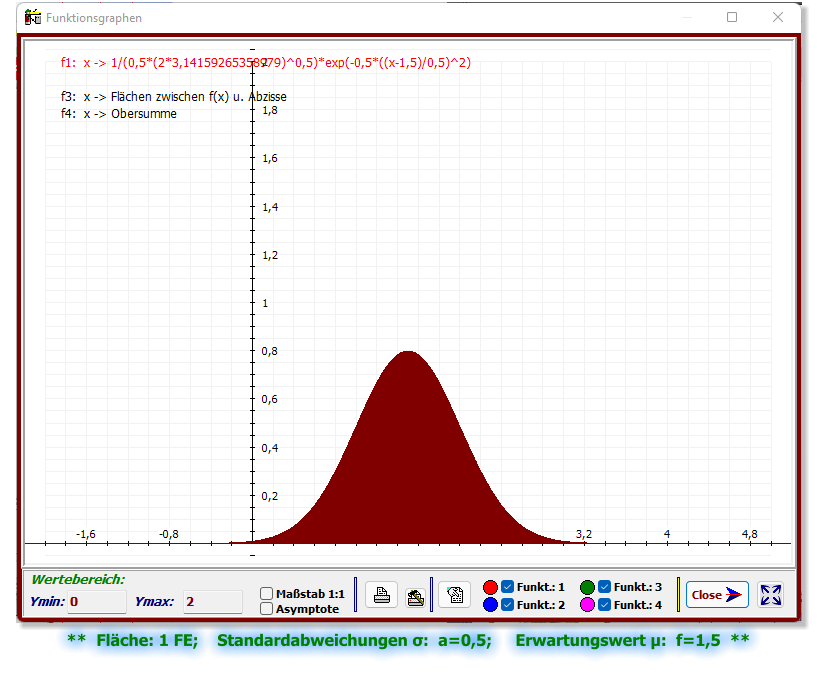
Der Wert der näherungsweise berechneten Fläche von 0,99999658 FE entspricht dem Wert 1 FE.
Wie erwartet, sind die Flächenwerte der einzelnen uneigentlichen Integrale ( ] -∞, ∞ [ ) der
Dichtefunktionen immer 1 FE.


Anwendungsbereich: Funktionen - Tabellen erstellen
Anwendungsbereich: Funktionen - Tabellen erstellen
Beispiele: Binomialkoeffizienten
Beispiele: Binomialkoeffizienten






Beispiel für eine Tabellen- bzw. Listenausgabe (Menü f:x->f(x); Tabelle erstellen)
Als ein exemplarisches Beispiel sollen hier alle Koeffizienten eines Binoms vom Grade n
berechnet werden.
Gesucht werden folglich die Werte für C
0
, C
1
, C
2
, C
3
, ....,C
n-2
, C
n-1
, C
n
Beispiel für n = 50.
Anmerkung: Binomialkoeffizientenfunktion n über k: T = bin( n | k ) mit n, k , k n
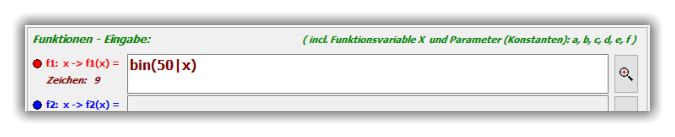
f(x) = bin( 50 | x ) mit (also alle ganzen Zahlen von 0 bis 50)
Hinweis: Da gilt, erscheinen nur für Zahlen ohne Komma Ergebnisse.
Eine Alternative wäre, die Argumente zu runden ( f(x) = bin( 50 | round( x ) ).
Anleitung: a. Funktionsterm im Fenster „Funktionen - Eingabe“ eingeben:
b. Im Fester „Tabelle erstellen“ den Definitionsbereich so wählen, dass die x-Werte die
natürlichen Zahlen 0 bis 50 annehmen können.
Anmerkung: Falls Sie nicht die Option Schrittweite wählen, beachten Sie, dass die Schrittweite selbst eine natürliche Zahl sein muss!
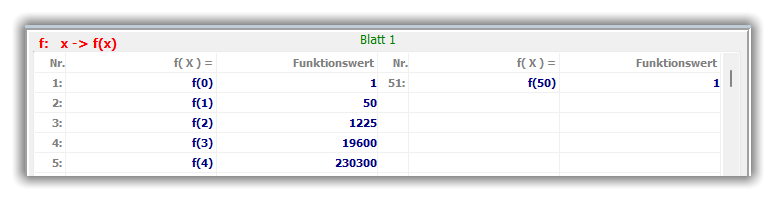
Ergebnis:
Die nachfolgenden Tabellenausschnitte listen die Werte der einzelnen Binomialkoeffizienten C
k
auf.
Folglich gilt:
C
0
= 1,
C
1
= 50,
C
2
= 1225,
C
3
= 19600,
C
23
= 108.043.253.365.600,
C
24
= 121.548.660.036.300,
C
25
= 126.410.606.437.752,
C
27
= 108.043.253.365.600,
C
26
= 121.548.660.036.300
usw.
und somit:
(a+b)
50
= 1a
50
b
0
+ 50a
49
b
1
+ 1225a
48
b
2
+ 19600a
47
b
3
+ ... + 19600a
3
b
47
+ 1225a
48
b
2
+ 50a
49
b
1
+ 1a
0
b
50
bzw.:
Die generierte Tabelle - Liste - kann auch auf dem Drucker ausgegeben werden.
Falls Koeffizienten für mehrere Binome bestimmt werden sollen, kann auch der folgende
allgemeine Ansatz gewählt werde:
- f(x) = bin( a | x ), wobei der Parameter a (im Prinzip) für n steht.
- Definitionsbereich [ x
a
; x
b
] mit x
a
= 0 und x
b
= a (a < 101, da maximal 100 Tabellenzeilen).
- Delta x = 1 (x durchläuft dann nur die Werte 0, 1, 2, 3, 4, … , a-2, a-1, a).
Mit z. B. a = 74 (vorher eingegeben im Fenster „Funktionswerte mit X ....“) werden die
Koeffizienten C
0
, C
1
, C
2
, ... , C
73
und C
74
in der Tabelle ausgegeben.









Berechnung der Verteilungsfunktion:
Berechnung der Verteilungsfunktion:

Anleitung:
Anleitung:
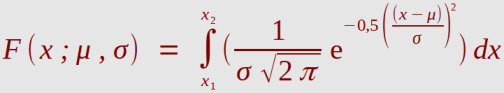
Beispiel: Stochastik
Beispiel: Stochastik
Beispiel: Stochastik
Beispiel: Stochastik
Die Verteilungsfunktion F(x;μ,σ) ist ein Integral, welches sich nicht analytisch auswerten lässt
[ erf(x) - Gausche Fehlerfunktion ]. Es lassen sich nun aber die Varianten der Normalverteilung
durch Standardisierung der Zufallsvariablen (Substitution) auf eine standardisierte Form bringen.
Für diese Standardnormalverteilung bzw. normierten Normalverteilung (0-1-Normalverteilung)
lassen sich Tabellen erstellen, mit denen die Berechnungen dann durchgeführt werden können.
Die Tabellenwerte der Standardnormalverteilung, diese sind im Internet reichlich vorhanden,
können durch das folgende Integral berechnet werden.
( Erwartungswert μ = 0, Standardabweichung σ = 1 )
Obiger Integrand f
1
: x → f(x) = 1/( 2*Pi )^0,5 * exp(-0,5*x^2)
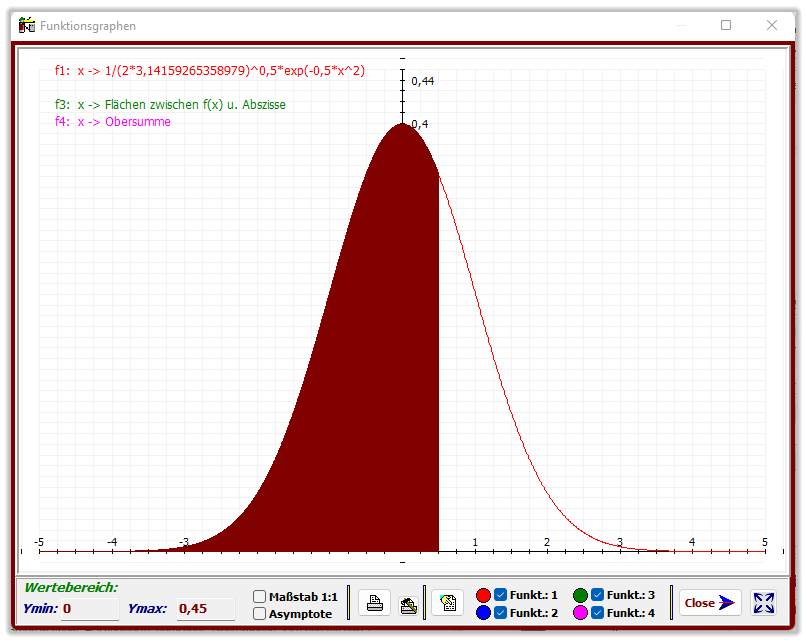
Tabellenwert für:
x
2
= 0,5
Φ
0;1
(0,5)=0,69146
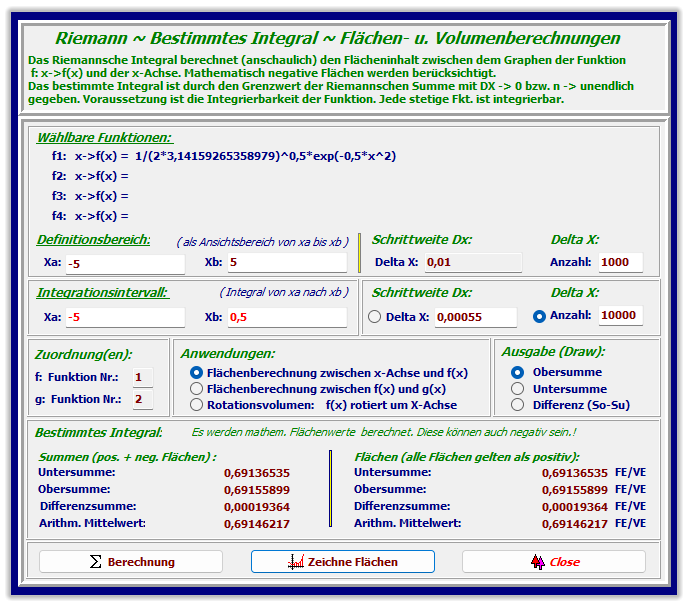
Berechnung (näherungsweise):
Tabellenwert für:
x
2
= 0,65
Φ
0;1
(0,65) = 0,74215
Berechnung (näherungsweise):
Tabellenwert für:
x
2
= 1,13
Φ
0;1
(1,13) = 0,87076
Berechnung (näherungsweise):
Tabellenwert für:
x
2
= 2,0
Φ
0;1
(2) = 0,97725
Berechnung (näherungsweise):
usw.
Anmerkung: Die Benutzung der Tabellen für Standardnormalverteilungen werde zugunsten der
rechnergestützten numerischen Integration immer weiter eingeschränkt.



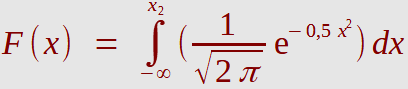
Tabellenwerte der Standardnormalverteilung:
Tabellenwerte der Standardnormalverteilung:
Beispiele für Tabellenwerte der Standardnormalverteilung:
Beispiele für Tabellenwerte der Standardnormalverteilung:

Ergebnisse:
Ergebnisse:











Rechner für Funktionen mit Variablen und Parametern.
Rechner für Funktionen mit Variablen und Parametern.