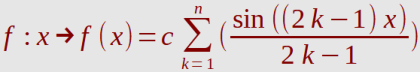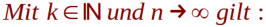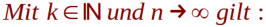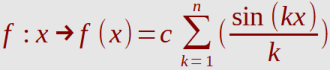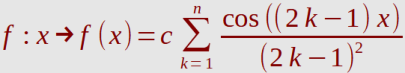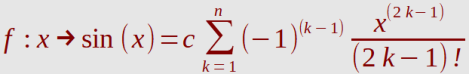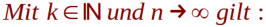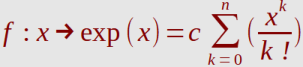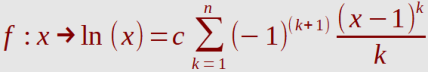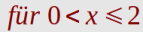Kleiner_Rechner.exe

Dieser Rechner für Funktionen ermöglicht es unter anderem, a. Wertetabellen zu erstellen, b. Funktionsgraphen zu plotten, c. Riemannsche Summen zu plotten bzw. bestimmte Integrale zu berechnen, d. Funktionsgraphen und die zugehörigen ersten drei Ableitungen grafisch auszugeben, e. Listen zu generieren usw. Alle angeführten Beispiele können durch Kopieren und Einfügen (copy and paste) direkt im Bereich „Funktioneneingabe“ in die Eingabefelder f 1 bis f 4 übernommen werden. Die hier zu sehenden Screenshots der Plotausgaben sind zur besseren Wiedergabe (Skalierung der Screenshots) bewusst nicht im Modus „Vollbildschirm“ erstellt worden. Eine zusätzliche Druckausgabe der Ergebnisse ist immer möglich. (Hinweis: Die Pfeile dienen auch als Links!) 1. Fourierreihen - Bildschirmausgaben: Beispiele für Fourierreihen (Partialsummen, Oberwellen, Konvergenz). Nicht nur für die Elektrotechnik! a. Zusammensetzung von Rechteckschwingungen durch Grund- und Oberwellen, b. Zusammensetzung von Sägezahnschwingungen durch Grund- und Oberwellen, c. Zusammensetzung von Dreiecksschwingungen durch Grund- und Oberwellen 2. Taylorreihe - Bildschirm: Beispiele für Taylorreihen - Mac Laurin – Reihen a. Sinusfunktion, b. e-Funktion x→e x (natürliche Exponentialfunktion, Basis e), c. Natürliche Logarithmusfunktion x→ln(x) ( x→log e (x) ) 3. Formeleditor - Demonstrationsbeispiel für die Formellänge: Exemplarisches Beispiel für die Leistungsfähigkeit des Formeleditors. Formel mit mehr als 9000 (ohne Blanks 7700) Zeichen.

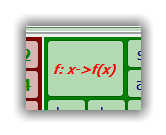
Der Faktor c bestimmt die Amplitudenhöhe. Dieser ist normalerweise 1! In den folgenden Beispielen wird für den Definitionsbereich empfohlen: D x = [ -8; 8 ] Für den Wertebereich (im Plotfenster einstellbar) empfiehlt sich W y = [ -1,1; 1,1 ] Näherungsweise Darstellung der Rechteckspannung (blau) für n=15 und c=1 Empfehlung: Kopieren Sie die nachfolgenden Beispiele und beurteilen Sie die Kurvenformen und das Konvergenzverhalten. Beispiel für eine Näherung mit n=2, c=0,5 f(x) = 1/2 * ( sin( 1*x )/1 + sin( 3*x )/3 ) Beispiel für eine Näherung mit n=5, c=0,5 f(x) = 1/2 * (sin(1*x)/1+sin(3*x)/3 + sin( 5*x )/5 ) Beispiel für eine Näherung mit n=15, c=0,5 f(x) = 1/2 * ( sin( x) + sin( 3*x)/ 3 + sin( 5*x)/ 5 + sin( 7*x)/ 7 + sin( 9*x)/ 9 + sin(11*x)/11 + sin(13*x)/13 + sin(15*x)/15 + sin(17*x)/17 + sin(19*x)/19 + sin(21*x)/21 + sin(23*x)/23 + sin(25*x)/25 + sin(27*x)/27 + sin(29*x)/29 + sin(31*x)/31 + sin(33*x)/33 ) Beispiel für eine Näherung mit n=25, c=0,5 f(x) = 1/2 * ( sin( x) + sin( 3*x)/ 3 + sin( 5*x)/ 5 + sin( 7*x)/ 7 + sin( 9*x)/ 9 + sin(11*x)/11 + sin(13*x)/13 + sin(15*x)/15 + sin(17*x)/17 + sin(19*x)/19 + sin(21*x)/21 + sin(23*x)/23 + sin(25*x)/25 + sin(27*x)/27 + sin(29*x)/29 + sin(31*x)/31 + sin(33*x)/33 + sin(35*x)/35 + sin(37*x)/37 + sin(39*x)/39 + sin(41*x)/41 + sin(43*x)/43 + sin(45*x)/45 + sin(47*x)/47 + sin(49*x)/49 ) Beispiel für eine Näherung mit n=50, c=0,5 f(x) = 1/2 * ( sin( x) + sin( 3*x)/ 3 + sin( 5*x)/ 5 + sin( 7*x)/ 7 + sin( 9*x)/ 9 + sin(11*x)/11 + sin(13*x)/13 + sin(15*x)/15 + sin(17*x)/17 + sin(19*x)/19 + sin(21*x)/21 + sin(23*x)/23 + sin(25*x)/25 + sin(27*x)/27 + sin(29*x)/29 + sin(31*x)/31 + sin(33*x)/33 + sin(35*x)/35 + sin(37*x)/37 + sin(39*x)/39 + sin(41*x)/41 + sin(43*x)/43 + sin(45*x)/45 + sin(47*x)/47 + sin(49*x)/49 + sin(51*x)/51 + sin(53*x)/53 + sin(55*x)/55 + sin(57*x)/57 + sin(59*x)/59 + sin(61*x)/61 + sin(63*x)/63 + sin(65*x)/65 + sin(67*x)/67 + sin(69*x)/69 + sin(71*x)/71 + sin(73*x)/73 + sin(75*x)/75 + sin(77*x)/77 + sin(79*x)/79 + sin(81*x)/81 + sin(83*x)/83 + sin(85*x)/85 + sin(87*x)/87 + sin(89*x)/89 + sin(91*x)/91 + sin(93*x)/93 + sin(95*x)/95 + sin(97*x)/97 + sin(99*x)/99 ) Der Faktor c bestimmt die Amplitudenhöhe. Dieser ist normalerweise 1! 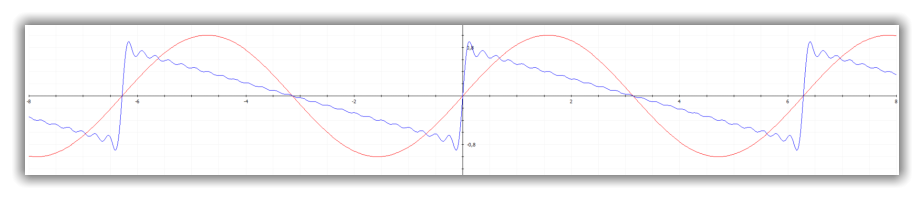In den folgenden Beispielen wird für den Definitionsbereich empfohlen: D(x) = [ -7; 7 ] Näherungsweise Darstellung der Sägezahnspannung (blau) für n=25 und c=0,5 Empfehlung: Kopieren Sie die nachfolgenden Beispiele und beurteilen Sie die Kurvenformen und das Konvergenzverhalten. Beispiel für eine Näherung mit n=2; c=1/3 f(x) = 1/3 * ( sin(x)/1 + sin(2*x)/2 ) Beispiel für eine Näherung mit n=5; c=1/3 f(x) = 1/3*( sin(x)+sin(2*x)/2+sin(3*x)/3+sin(4*x)/4+sin(5*x)/5 ) Beispiel für eine Näherung mit n=15; c=1/3 f(x) = 1/3*( sin( x ) + sin( 2*x)/ 2 + sin( 3*x)/ 3 + sin( 4*x)/ 4 + sin( 5*x)/ 5 + sin( 6*x)/ 6 + sin( 7*x)/ 7 + sin( 8*x)/ 8 + sin( 9*x)/ 9 + sin(10*x)/10 + sin(11*x)/11 + sin(12*x)/12 + sin(13*x)/13 + sin(14*x)/14 + sin(15*x)/15 ) Beispiel für eine Näherung mit n=25; c=1/3 f(x) = 1/3*( sin( x) + sin( 2*x)/ 2 + sin( 3*x)/ 3 + sin( 4*x)/ 4 + sin( 5*x)/ 5 + sin( 6*x)/ 6 + sin( 7*x)/ 7 + sin( 8*x)/ 8 + sin( 9*x)/ 9 + sin(10*x)/10 + sin(11*x)/11 + sin(12*x)/12 + sin(13*x)/13 + sin(14*x)/14 + sin(15*x)/15 + sin(16*x)/16 + sin(17*x)/17 + sin(18*x)/18 + sin(19*x)/19 + sin(20*x)/20 + sin(21*x)/21 + sin(22*x)/22 + sin(23*x)/23 + sin(24*x)/24 + sin(25*x)/25 ) Der Faktor c bestimmt die Amplitudenhöhe. Dieser ist normalerweise 1! 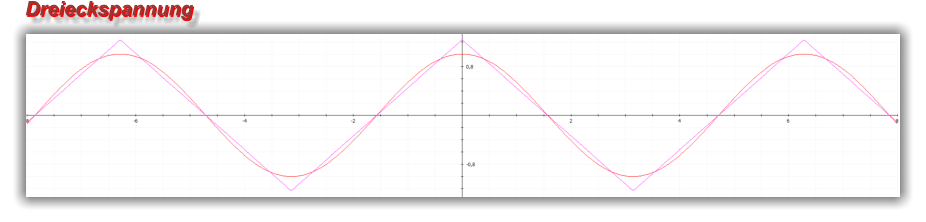In den folgenden Beispielen wird für den Definitionsbereich empfohlen: D(x) = [ -7; 7 ] Näherungsweise Darstellung der Dreiecksspannung (grün) für n=25 und c=1 Empfehlung: Kopieren Sie die nachfolgenden Beispiele und beurteilen Sie die Kurvenformen und das Konvergenzverhalten. Beispiel für eine Näherung mit n=2; C=1/2 f(x) = 1/2 * ( cos(1*x)/1^2 + cos(3*x)/3^2 ) Beispiel für eine Näherung mit n=5; C=1/2 f(x) = 1/2*( cos(1*x)/1^2 + cos(3*x)/3^2 + cos(5*x)/5^2 + cos(7*x)/7^2 + cos(9*x)/9^2 ) Beispiel für eine Näherung mit n=15; C=1/2 f(x) = 1/2*(cos( 1*x)/ 1^2 + cos( 3*x)/ 3^2 + cos( 5*x)/ 5^2 + cos( 7*x)/ 7^2 + cos( 9*x)/ 9^2 + cos(11*x)/11^2 + cos(13*x)/13^2 + cos(15*x)/15^2 + cos(17*x)/17^2 + cos(19*x)/19^2 + cos(21*x)/21^2 + cos(23*x)/23^2 + cos(25*x)/25^2 + cos(27*x)/27^2 + cos(29*x)/29^2 ) Beispiel n=25; C=1/2 f(x) = 1/2*(cos( 1*x)/ 1^2 + cos( 3*x)/ 3^2 + cos( 5*x)/ 5^2 + cos( 7*x)/ 7^2 + cos( 9*x)/ 9^2 + cos(11*x)/11^2 + cos(13*x)/13^2 + cos(15*x)/15^2 + cos(17*x)/17^2 + cos(19*x)/19^2 + cos(21*x)/21^2 + cos(23*x)/23^2 + cos(25*x)/25^2 + cos(27*x)/27^2 + cos(29*x)/29^2 + cos(31*x)/31^2 + cos(33*x)/33^2 + cos(35*x)/35^2 + cos(37*x)/37^2 + cos(39*x)/39^2 + cos(41*x)/41^2 + cos(43*x)/43^2 + cos(45*x)/45^2 + cos(47*x)/47^2 + cos(49*x)/49^2 )

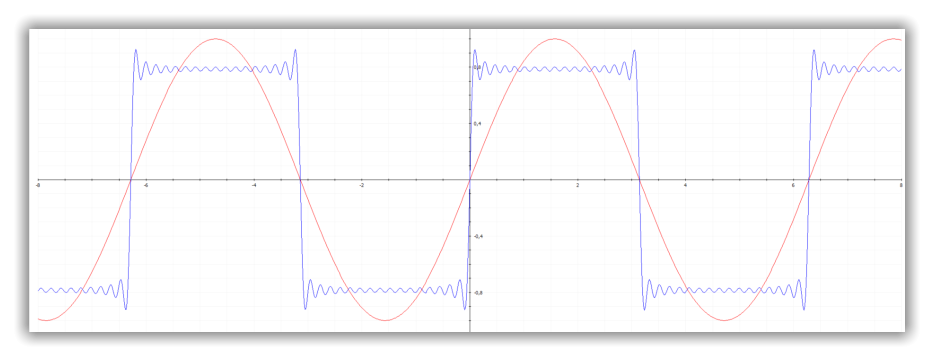
Die obige Plotausgabe zeigt die Sinusfunktion (rot) und die Näherungen (Taylorreihe) für n=3 (blau), n=5 (grün) und n=15 (magenta). Der Faktor c bestimmt die Amplitudenhöhe. Dieser ist normalerweise 1! In den folgenden Beispielen wird für den Definitionsbereich empfohlen: D(x) = [ -7; 7 ]. Zur weiteren Betrachtung sollte auch ein größeres Intervall, z. B. xl = -20 und xr = 20, gewählt werden. Beispiel n=3; C=1/2 f(x) = 1/2*( x^01/n!(01) - x^03/n!(03) + x^05/n!(05) ) Beispiel n=5; C=1/2 f(x) = 1/2*( x - x^03/n!(03) + x^05/n!(05) - x^07/n!(07) + x^09/n!(09)) Beispiel n=15; C=1/2 f(x) = 1/2*( x - x^03/n!(03) + x^05/n!(05) - x^07/n!(07) + x^09/n!(09) - x^11/n!(11) + x^13/n!(13) - x^15/n!(15) + x^17/n!(17) - x^19/n!(19) + x^21/n!(21) - x^23/n!(23) + x^25/n!(25) - x^27/n!(27) + x^29/n!(29)) Beispiel n=30; C=1/2 f(x) = 1/2*( x - x^03/n!(03) + x^05/n!(05) - x^07/n!(07) + x^09/n!(09) - x^11/n!(11) + x^13/n!(13) - x^15/n!(15) + x^17/n!(17) - x^19/n!(19) + x^21/n!(21) - x^23/n!(23) + x^25/n!(25) - x^27/n!(27) + x^29/n!(29) - x^31/n!(31) + x^33/n!(33) - x^35/n!(35) + x^37/n!(37) - x^39/n!(39) + x^41/n!(41) - x^43/n!(43) + x^45/n!(45) - x^47/n!(47) + x^49/n!(49) - x^51/n!(51) + x^53/n!(53) - x^55/n!(55) + x^57/n!(57) - x^59/n!(59)) Auch die natürliche Exponentialfunktion (x→e x , e = Eulersche Zahl) lässt sich durch eine unendliche Reihe darstellen. Der Faktor c ist normalerweise 1! Wie Sie mit den beiden Beispielen für die Näherungsberechnung mit n=4 und n=14 feststellen können, konvergiert die Reihe im Bereich des Ursprungs sehr schnell. 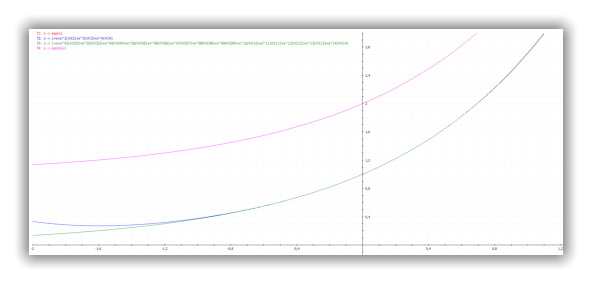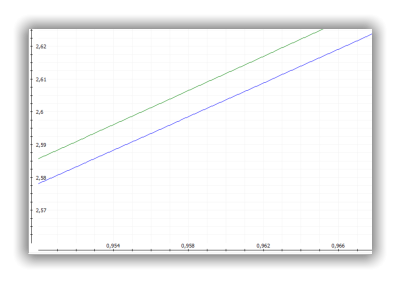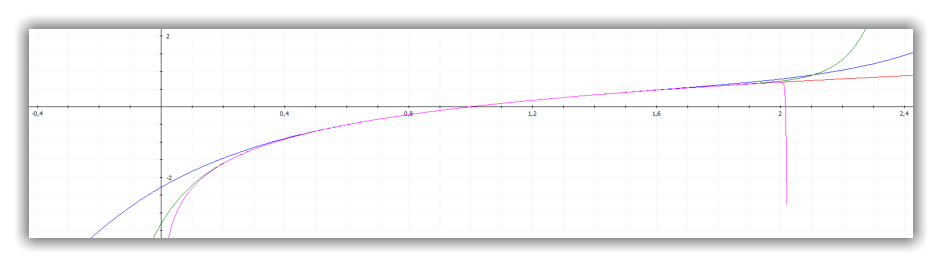Beispiel n=4 (5 Summanden) f(x) = 1 + x + X^2/n!(2) + X^3/n!(3) + X^4/n!(4) Beispiel n=14 (15 Summanden) f(x) = 1 + x + X^02/n!(02) + X^03/n!(03) + X^04/n!(04) + X^05/n!(05) + X^06/n!(06) + X^07/n!(07) + X^08/n!(08) + X^09/n!(09) + X^10/n!(10) + X^11/n!(11) + X^12/n!(12) + X^13/n!(13) + X^14/n!(14) Die obige linke Plotausgabe zeigt die e-Funktion (rot) und die Näherungen (Taylorreihe) für n=4 (blau) und n=14 (grün). Da die rote Funktion von der grünen Fkt. komplett überlagert wird, ist zum Vergleich der Verlauf der e-Funktion x → f(x) = e x + 1 (magenta) ebenfalls dargestellt. Die rechte Plottausgabe zeigt den Ausschnitt x ∈ [ 0,95; 0,968 ] und y ∈ [ 2,56; 2,625 ]. Wie die Beispiele zeigen, konvergiert die Reihe sehr schnell. Die Funktion (Logarithmus Naturalis) lässt sich durch die nachfolgende unendliche Reihe im Bereich 0 < x ≤ 2 darstellen. Der Faktor c ist normalerweise 1! Da die Reihe im Definitionsbereich eingeschränkt ist, wird für diese Beispiele der Definitionsbereich D(x) = [ -0,5; 2,5 ] empfohlen: Wie auch die Beispiele zeigen, konvergiert die Reihe sehr langsam. Beispiel n=5 f(x) = (X-1) - (X-1)^2/2 + (X-1)^3/3 - (X-1)^4/4 + (X-1)^5/5 Beispiel n=15 f(x) = (X-1) – (X-1)^ 2/ 2 + (X-1)^ 3/ 3 – (X-1)^ 4/ 4 + (X-1)^ 5/ 5 – (X-1)^ 6/ 6 + (X-1)^ 7/ 7 – (X-1)^ 8/ 8 + (X-1)^ 9/ 9 – (X-1)^10/10 + (X-1)^11/11 – (X-1)^12/12 + (X-1)^13/13 – (X-1)^14/14 + (X-1)^15/15 Beispiel n=400 (längere Rechenzeit, siehe unten!) f: x->f(x)= (X-1) – (X-1)^ 2/ 2 + (X-1)^ 3/ 3 – (X-1)^ 4/ 4 + (X-1)^ 5/ 5 – (X-1)^ 6/ 6 + (X-1)^ 7/ 7 – (X-1)^ 8/ 8 + (X-1)^ 9/ 9 – (X-1)^ 10/ 10 + (X-1)^ 11/ 11 – (X-1)^ 12/ 12 + (X-1)^ 13/ 13 – (X-1)^ 14/ 14 + (X-1)^ 15/ 15 - (X-1)^ 16/ 16 + (X-1)^ 17/ 17 – (X-1)^ 18/ 18 + (X-1)^ 19/ 19 – (X-1)^ 20/ 20 + (X-1)^ 21/ 21 – (X-1)^ 22/ 22 + (X-1)^ 23/ 23 – (X-1)^ 24/ 24 + (X-1)^ 25/ 25 - (X-1)^ 26/ 26 + (X-1)^ 27/ 27 – (X-1)^ 28/ 28 + (X-1)^ 29/ 29 – (X-1)^ 30/ 30 + (X-1)^ 31/ 31 – (X-1)^ 32/ 32 + (X-1)^ 33/ 33 – (X-1)^ 34/ 34 + (X-1)^ 35/ 35 - (X-1)^ 36/ 36 + (X-1)^ 37/ 37 – (X-1)^ 38/ 38 + (X-1)^ 39/ 39 – (X-1)^ 40/ 40 + (X-1)^ 41/ 41 – (X-1)^ 42/ 42 + (X-1)^ 43/ 43 – (X-1)^ 44/ 44 + (X-1)^ 45/ 45 - (X-1)^ 46/ 46 + (X-1)^ 47/ 47 – (X-1)^ 48/ 48 + (X-1)^ 49/ 49 – (X-1)^ 50/ 50 + (X-1)^ 51/ 51 – (X-1)^ 52/ 52 + (X-1)^ 53/ 53 – (X-1)^ 54/ 54 + (X-1)^ 55/ 55 - (X-1)^ 56/ 56 + (X-1)^ 57/ 57 – (X-1)^ 58/ 58 + (X-1)^ 59/ 59 – (X-1)^ 60/ 60 + (X-1)^ 61/ 61 – (X-1)^ 62/ 62 + (X-1)^ 63/ 63 – (X-1)^ 64/ 64 + (X-1)^ 65/ 65 - (X-1)^ 66/ 66 + (X-1)^ 67/ 67 – (X-1)^ 68/ 68 + (X-1)^ 69/ 69 – (X-1)^ 70/ 70 + (X-1)^ 71/ 71 – (X-1)^ 72/ 72 + (X-1)^ 73/ 73 – (X-1)^ 74/ 74 + (X-1)^ 75/ 75 - (X-1)^ 76/ 76 + (X-1)^ 77/ 77 – (X-1)^ 78/ 78 + (X-1)^ 79/ 79 – (X-1)^ 80/ 80 + (X-1)^ 81/ 81 – (X-1)^ 82/ 82 + (X-1)^ 83/ 83 – (X-1)^ 84/ 84 + (X-1)^ 85/ 85 - (X-1)^ 86/ 86 + (X-1)^ 87/ 87 – (X-1)^ 88/ 88 + (X-1)^ 89/ 89 – (X-1)^ 90/ 90 + (X-1)^ 91/ 91 – (X-1)^ 92/ 92 + (X-1)^ 93/ 93 – (X-1)^ 94/ 94 + (X-1)^ 95/ 95 - (X-1)^ 96/ 96 + (X-1)^ 97/ 97 – (X-1)^ 98/ 98 + (X-1)^ 99/ 99 – (X-1)^100/100 + (X-1)^101/101 - (X-1)^102/102 + (X-1)^103/103 - (X-1)^104/104 + (X-1)^105/105 - (X-1)^106/106 + (X-1)^107/107 - (X-1)^108/108 + (X-1)^109/109 – (X-1)^110/110 + (X-1)^111/111 - (X-1)^112/112 + (X-1)^113/113 - (X-1)^114/114 + (X-1)^115/115 - (X-1)^116/116 + (X-1)^117/117 - (X-1)^118/118 + (X-1)^119/119 – (X-1)^120/120 + (X-1)^121/101 - (X-1)^122/102 + (X-1)^123/123 - (X-1)^124/124 + (X-1)^125/125 - (X-1)^126/106 + (X-1)^127/107 - (X-1)^128/128 + (X-1)^129/129 – (X-1)^130/130 + (X-1)^131/111 - (X-1)^132/112 + (X-1)^133/133 - (X-1)^134/134 + (X-1)^135/135 - (X-1)^136/116 + (X-1)^137/117 - (X-1)^138/138 + (X-1)^139/139 – (X-1)^140/140 + (X-1)^141/141 - (X-1)^142/142 + (X-1)^143/143 - (X-1)^144/144 + (X-1)^145/145 - (X-1)^146/146 + (X-1)^147/147 - (X-1)^148/148 + (X-1)^149/149 – (X-1)^150/150 + (X-1)^151/151 - (X-1)^152/152 + (X-1)^153/153 - (X-1)^154/154 + (X-1)^155/155 - (X-1)^156/156 + (X-1)^157/157 - (X-1)^158/158 + (X-1)^159/159 – (X-1)^160/160 + (X-1)^161/161 - (X-1)^162/162 + (X-1)^163/163 - (X-1)^164/164 + (X-1)^165/165 - (X-1)^166/166 + (X-1)^167/167 - (X-1)^168/168 + (X-1)^169/169 – (X-1)^170/170 + (X-1)^171/171 - (X-1)^172/172 + (X-1)^173/173 - (X-1)^174/174 + (X-1)^175/175 - (X-1)^176/176 + (X-1)^177/177 - (X-1)^178/178 + (X-1)^179/179 – (X-1)^180/180 + (X-1)^181/181 - (X-1)^182/182 + (X-1)^183/183 - (X-1)^184/184 + (X-1)^185/185 - (X-1)^186/186 + (X-1)^187/187 - (X-1)^188/188 + (X-1)^189/189 – (X-1)^190/190 + (X-1)^191/191 - (X-1)^192/192 + (X-1)^193/193 - (X-1)^194/194 + (X-1)^195/195 - (X-1)^196/196 + (X-1)^197/197 - (X-1)^198/198 + (X-1)^199/199 – (X-1)^200/200 + (X-1)^201/201 - (X-1)^202/202 + (X-1)^203/203 - (X-1)^204/204 + (X-1)^205/205 - (X-1)^206/206 + (X-1)^207/207 - (X-1)^208/208 + (X-1)^209/209 – (X-1)^210/210 + (X-1)^211/211 - (X-1)^212/212 + (X-1)^213/213 - (X-1)^214/214 + (X-1)^215/215 - (X-1)^216/216 + (X-1)^217/217 - (X-1)^218/218 + (X-1)^219/219 – (X-1)^220/220 + (X-1)^221/201 - (X-1)^222/202 + (X-1)^223/223 - (X-1)^224/224 + (X-1)^225/225 - (X-1)^226/206 + (X-1)^227/207 - (X-1)^228/228 + (X-1)^229/229 – (X-1)^230/230 + (X-1)^231/211 - (X-1)^232/212 + (X-1)^233/233 - (X-1)^234/234 + (X-1)^235/235 - (X-1)^236/216 + (X-1)^237/217 - (X-1)^238/238 + (X-1)^239/239 – (X-1)^240/240 + (X-1)^241/241 - (X-1)^242/242 + (X-1)^243/243 - (X-1)^244/244 + (X-1)^245/245 - (X-1)^246/246 + (X-1)^247/247 - (X-1)^248/248 + (X-1)^249/249 – (X-1)^250/250 + (X-1)^251/251 - (X-1)^252/252 + (X-1)^253/253 - (X-1)^254/254 + (X-1)^255/255 - (X-1)^256/256 + (X-1)^257/257 - (X-1)^258/258 + (X-1)^259/259 – (X-1)^260/260 + (X-1)^261/261 - (X-1)^262/262 + (X-1)^263/263 - (X-1)^264/264 + (X-1)^265/265 - (X-1)^266/266 + (X-1)^267/267 - (X-1)^268/268 + (X-1)^269/269 – (X-1)^270/270 + (X-1)^271/271 - (X-1)^272/272 + (X-1)^273/273 - (X-1)^274/274 + (X-1)^275/275 - (X-1)^276/276 + (X-1)^277/277 - (X-1)^278/278 + (X-1)^279/279 – (X-1)^280/280 + (X-1)^281/281 - (X-1)^282/282 + (X-1)^283/283 - (X-1)^284/284 + (X-1)^285/285 - (X-1)^286/286 + (X-1)^287/287 - (X-1)^288/288 + (X-1)^289/289 – (X-1)^290/290 + (X-1)^291/291 - (X-1)^292/292 + (X-1)^293/293 - (X-1)^294/294 + (X-1)^295/295 - (X-1)^296/296 + (X-1)^297/297 - (X-1)^298/298 + (X-1)^299/299 – (X-1)^300/300 + (X-1)^301/301 - (X-1)^302/302 + (X-1)^303/303 - (X-1)^304/304 + (X-1)^305/305 - (X-1)^306/306 + (X-1)^307/307 - (X-1)^308/308 + (X-1)^309/309 – (X-1)^310/310 + (X-1)^311/311 - (X-1)^312/312 + (X-1)^313/313 - (X-1)^314/314 + (X-1)^315/315 - (X-1)^316/316 + (X-1)^317/317 - (X-1)^318/318 + (X-1)^319/319 – (X-1)^320/320 + (X-1)^321/301 - (X-1)^322/302 + (X-1)^323/323 - (X-1)^324/324 + (X-1)^325/325 - (X-1)^326/306 + (X-1)^327/307 - (X-1)^328/328 + (X-1)^329/329 – (X-1)^330/330 + (X-1)^331/311 - (X-1)^332/312 + (X-1)^333/333 - (X-1)^334/334 + (X-1)^335/335 - (X-1)^336/316 + (X-1)^337/317 - (X-1)^338/338 + (X-1)^339/339 – (X-1)^340/340 + (X-1)^341/341 - (X-1)^342/342 + (X-1)^343/343 - (X-1)^344/344 + (X-1)^345/345 - (X-1)^346/346 + (X-1)^347/347 - (X-1)^348/348 + (X-1)^349/349 – (X-1)^350/350 + (X-1)^351/351 - (X-1)^352/352 + (X-1)^353/353 - (X-1)^354/354 + (X-1)^355/355 - (X-1)^356/356 + (X-1)^357/357 - (X-1)^358/358 + (X-1)^359/359 – (X-1)^360/360 + (X-1)^361/361 - (X-1)^362/362 + (X-1)^363/363 - (X-1)^364/364 + (X-1)^365/365 - (X-1)^366/366 + (X-1)^367/367 - (X-1)^368/368 + (X-1)^369/369 – (X-1)^370/370 + (X-1)^371/371 - (X-1)^372/372 + (X-1)^373/373 - (X-1)^374/374 + (X-1)^375/375 - (X-1)^376/376 + (X-1)^377/377 - (X-1)^378/378 + (X-1)^379/379 – (X-1)^380/380 + (X-1)^381/381 - (X-1)^382/382 + (X-1)^383/383 - (X-1)^384/384 + (X-1)^385/385 - (X-1)^386/386 + (X-1)^387/387 - (X-1)^388/388 + (X-1)^389/389 – (X-1)^390/390 + (X-1)^391/391 - (X-1)^392/392 + (X-1)^393/393 - (X-1)^394/394 + (X-1)^395/395 - (X-1)^396/396 + (X-1)^397/397 - (X-1)^398/398 + (X-1)^399/399 – (X-1)^400/400 Als Definitionsbereich wird xl = -0,5 und xr = 2,5 empfohlen. Hinweis: Bitte beachten Sie die Formellänge (ohne Blanks) von über 5500 Zeichen! Aufgrund des zusätzlichen extrem hohen Rechenaufwandes – Potenzen mit Exponenten in der Größe bis 400 – können hier schon mal Rechenzeiten von 15 Sekunden erwartet werden! Die obige Plotausgabe zeigt die Logarithmusfunktion (ln(x), rot) und die Näherungen (Taylorreihe) für n=5 (blau), n=15 (grün) und n=400 (magenta). Der eingeschränkte Definitionsbereich ist gut erkennbar.

Grundsatz: Jede periodische Funktion, die sich als Schwingung darstellt, lässt sich als Summe (Überlagerungen) der Grundschwingung und den zugehörigen Oberschwingungen (Oberwellen) generieren. Fourierreihen sind unendliche Reihen und haben eine wesentliche Bedeutung in der Technik. Dieses gilt auch speziell für die Elektrotechnik, z. B.: in der Filtertechnik. Nachfolgend werden exemplarisch drei in der Elektrotechnik weitverbreitete Kurvenformen - Rechteckkurve, Dreieckkurve und Sägezahnkurve - mathematisch behandelt. Aussagen über das Konvergenzverhalten sowie über den Einfluss der Anzahl der Oberwellen usw. können hier einsichtig getroffen werden. Anmerkung: Bitte beachten Sie bei der Analyse von abgebrochenen Fourierreihen das „Gibbs’sches Phänomen“ (Gibbssches Ringing)!

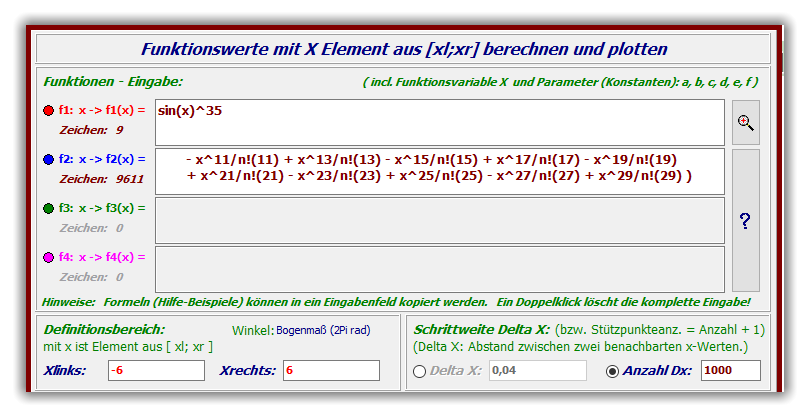
Dieses (etwas künstliche) Beispiel einer langen Formel mit mehr als 9000 (ohne Leerzeichen mehr als 7700) Zeichen zeigt, dass eine Formel von der Länge bzw. Anzahl der Terme praktisch nicht beschränkt ist. Als Definitionsbereich wird xl = -6 und xr = 6 empfohlen. Im Folgenden wird näherungsweise die Funktionsgleichung f: x → sin 35 (x), also f(x) = sin(x)^35 bzw. f(x) = sin(x) * sin(x) * sin(x) * sin(x) * sin(x) * sin(x) * sin(x) * sin(x) * sin(x) * sin(x) * sin(x) * sin(x) * sin(x) * sin(x) * sin(x) * sin(x) * sin(x) * sin(x) * sin(x) * sin(x) * sin(x) * sin(x) * sin(x) * sin(x) * sin(x) * sin(x) * sin(x) * sin(x) * sin(x) * sin(x) * sin(x) * sin(x) * sin(x) * sin(x) * sin(x) als Näherung mit der Taylorreihe für n=15 berechnet: Bitte beachten Sie, diese Funktionsgleichung besitzt 585 Glieder die u. a. alle Fakultäten und Potenzen enthalten → längere Rechenzeit, siehe unten ! f(x)= ( x - x^03/n!(03) + x^05/n!(05) - x^07/n!(07) + x^09/n!(09) - x^11/n!(11) + x^13/n!(13) - x^15/n!(15) + x^17/n!(17) - x^19/n!(19) + x^21/n!(21) - x^23/n!(23) + x^25/n!(25) - x^27/n!(27) + x^29/n!(29) ) * ( x - x^03/n!(03) + x^05/n!(05) - x^07/n!(07) + x^09/n!(09) - x^11/n!(11) + x^13/n!(13) - x^15/n!(15) + x^17/n!(17) - x^19/n!(19) + x^21/n!(21) - x^23/n!(23) + x^25/n!(25) - x^27/n!(27) + x^29/n!(29) ) * ( x - x^03/n!(03) + x^05/n!(05) - x^07/n!(07) + x^09/n!(09) - x^11/n!(11) + x^13/n!(13) - x^15/n!(15) + x^17/n!(17) - x^19/n!(19) + x^21/n!(21) - x^23/n!(23) + x^25/n!(25) - x^27/n!(27) + x^29/n!(29) ) * ( x - x^03/n!(03) + x^05/n!(05) - x^07/n!(07) + x^09/n!(09) - x^11/n!(11) + x^13/n!(13) - x^15/n!(15) + x^17/n!(17) - x^19/n!(19) + x^21/n!(21) - x^23/n!(23) + x^25/n!(25) - x^27/n!(27) + x^29/n!(29) ) * ( x - x^03/n!(03) + x^05/n!(05) - x^07/n!(07) + x^09/n!(09) - x^11/n!(11) + x^13/n!(13) - x^15/n!(15) + x^17/n!(17) - x^19/n!(19) + x^21/n!(21) - x^23/n!(23) + x^25/n!(25) - x^27/n!(27) + x^29/n!(29) ) * ( x - x^03/n!(03) + x^05/n!(05) - x^07/n!(07) + x^09/n!(09) - x^11/n!(11) + x^13/n!(13) - x^15/n!(15) + x^17/n!(17) - x^19/n!(19) + x^21/n!(21) - x^23/n!(23) + x^25/n!(25) - x^27/n!(27) + x^29/n!(29) ) * ( x - x^03/n!(03) + x^05/n!(05) - x^07/n!(07) + x^09/n!(09) - x^11/n!(11) + x^13/n!(13) - x^15/n!(15) + x^17/n!(17) - x^19/n!(19) + x^21/n!(21) - x^23/n!(23) + x^25/n!(25) - x^27/n!(27) + x^29/n!(29) ) * ( x - x^03/n!(03) + x^05/n!(05) - x^07/n!(07) + x^09/n!(09) - x^11/n!(11) + x^13/n!(13) - x^15/n!(15) + x^17/n!(17) - x^19/n!(19) + x^21/n!(21) - x^23/n!(23) + x^25/n!(25) - x^27/n!(27) + x^29/n!(29) ) * ( x - x^03/n!(03) + x^05/n!(05) - x^07/n!(07) + x^09/n!(09) - x^11/n!(11) + x^13/n!(13) - x^15/n!(15) + x^17/n!(17) - x^19/n!(19) + x^21/n!(21) - x^23/n!(23) + x^25/n!(25) - x^27/n!(27) + x^29/n!(29) ) * ( x - x^03/n!(03) + x^05/n!(05) - x^07/n!(07) + x^09/n!(09) - x^11/n!(11) + x^13/n!(13) - x^15/n!(15) + x^17/n!(17) - x^19/n!(19) + x^21/n!(21) - x^23/n!(23) + x^25/n!(25) - x^27/n!(27) + x^29/n!(29) ) * ( x - x^03/n!(03) + x^05/n!(05) - x^07/n!(07) + x^09/n!(09) - x^11/n!(11) + x^13/n!(13) - x^15/n!(15) + x^17/n!(17) - x^19/n!(19) + x^21/n!(21) - x^23/n!(23) + x^25/n!(25) - x^27/n!(27) + x^29/n!(29) ) * ( x - x^03/n!(03) + x^05/n!(05) - x^07/n!(07) + x^09/n!(09) - x^11/n!(11) + x^13/n!(13) - x^15/n!(15) + x^17/n!(17) - x^19/n!(19) + x^21/n!(21) - x^23/n!(23) + x^25/n!(25) - x^27/n!(27) + x^29/n!(29) ) * ( x - x^03/n!(03) + x^05/n!(05) - x^07/n!(07) + x^09/n!(09) - x^11/n!(11) + x^13/n!(13) - x^15/n!(15) + x^17/n!(17) - x^19/n!(19) + x^21/n!(21) - x^23/n!(23) + x^25/n!(25) - x^27/n!(27) + x^29/n!(29) ) * ( x - x^03/n!(03) + x^05/n!(05) - x^07/n!(07) + x^09/n!(09) - x^11/n!(11) + x^13/n!(13) - x^15/n!(15) + x^17/n!(17) - x^19/n!(19) + x^21/n!(21) - x^23/n!(23) + x^25/n!(25) - x^27/n!(27) + x^29/n!(29) ) * ( x - x^03/n!(03) + x^05/n!(05) - x^07/n!(07) + x^09/n!(09) - x^11/n!(11) + x^13/n!(13) - x^15/n!(15) + x^17/n!(17) - x^19/n!(19) + x^21/n!(21) - x^23/n!(23) + x^25/n!(25) - x^27/n!(27) + x^29/n!(29) ) * ( x - x^03/n!(03) + x^05/n!(05) - x^07/n!(07) + x^09/n!(09) - x^11/n!(11) + x^13/n!(13) - x^15/n!(15) + x^17/n!(17) - x^19/n!(19) + x^21/n!(21) - x^23/n!(23) + x^25/n!(25) - x^27/n!(27) + x^29/n!(29) ) * ( x - x^03/n!(03) + x^05/n!(05) - x^07/n!(07) + x^09/n!(09) - x^11/n!(11) + x^13/n!(13) - x^15/n!(15) + x^17/n!(17) - x^19/n!(19) + x^21/n!(21) - x^23/n!(23) + x^25/n!(25) - x^27/n!(27) + x^29/n!(29) ) * ( x - x^03/n!(03) + x^05/n!(05) - x^07/n!(07) + x^09/n!(09) - x^11/n!(11) + x^13/n!(13) - x^15/n!(15) + x^17/n!(17) - x^19/n!(19) + x^21/n!(21) - x^23/n!(23) + x^25/n!(25) - x^27/n!(27) + x^29/n!(29) ) * ( x - x^03/n!(03) + x^05/n!(05) - x^07/n!(07) + x^09/n!(09) - x^11/n!(11) + x^13/n!(13) - x^15/n!(15) + x^17/n!(17) - x^19/n!(19) + x^21/n!(21) - x^23/n!(23) + x^25/n!(25) - x^27/n!(27) + x^29/n!(29) ) * ( x - x^03/n!(03) + x^05/n!(05) - x^07/n!(07) + x^09/n!(09) - x^11/n!(11) + x^13/n!(13) - x^15/n!(15) + x^17/n!(17) - x^19/n!(19) + x^21/n!(21) - x^23/n!(23) + x^25/n!(25) - x^27/n!(27) + x^29/n!(29) ) * ( x - x^03/n!(03) + x^05/n!(05) - x^07/n!(07) + x^09/n!(09) - x^11/n!(11) + x^13/n!(13) - x^15/n!(15) + x^17/n!(17) - x^19/n!(19) + x^21/n!(21) - x^23/n!(23) + x^25/n!(25) - x^27/n!(27) + x^29/n!(29) ) * ( x - x^03/n!(03) + x^05/n!(05) - x^07/n!(07) + x^09/n!(09) - x^11/n!(11) + x^13/n!(13) - x^15/n!(15) + x^17/n!(17) - x^19/n!(19) + x^21/n!(21) - x^23/n!(23) + x^25/n!(25) - x^27/n!(27) + x^29/n!(29) ) * ( x - x^03/n!(03) + x^05/n!(05) - x^07/n!(07) + x^09/n!(09) - x^11/n!(11) + x^13/n!(13) - x^15/n!(15) + x^17/n!(17) - x^19/n!(19) + x^21/n!(21) - x^23/n!(23) + x^25/n!(25) - x^27/n!(27) + x^29/n!(29) ) * ( x - x^03/n!(03) + x^05/n!(05) - x^07/n!(07) + x^09/n!(09) - x^11/n!(11) + x^13/n!(13) - x^15/n!(15) + x^17/n!(17) - x^19/n!(19) + x^21/n!(21) - x^23/n!(23) + x^25/n!(25) - x^27/n!(27) + x^29/n!(29) ) * ( x - x^03/n!(03) + x^05/n!(05) - x^07/n!(07) + x^09/n!(09) - x^11/n!(11) + x^13/n!(13) - x^15/n!(15) + x^17/n!(17) - x^19/n!(19) + x^21/n!(21) - x^23/n!(23) + x^25/n!(25) - x^27/n!(27) + x^29/n!(29) ) * ( x - x^03/n!(03) + x^05/n!(05) - x^07/n!(07) + x^09/n!(09) - x^11/n!(11) + x^13/n!(13) - x^15/n!(15) + x^17/n!(17) - x^19/n!(19) + x^21/n!(21) - x^23/n!(23) + x^25/n!(25) - x^27/n!(27) + x^29/n!(29) ) * ( x - x^03/n!(03) + x^05/n!(05) - x^07/n!(07) + x^09/n!(09) - x^11/n!(11) + x^13/n!(13) - x^15/n!(15) + x^17/n!(17) - x^19/n!(19) + x^21/n!(21) - x^23/n!(23) + x^25/n!(25) - x^27/n!(27) + x^29/n!(29) ) * ( x - x^03/n!(03) + x^05/n!(05) - x^07/n!(07) + x^09/n!(09) - x^11/n!(11) + x^13/n!(13) - x^15/n!(15) + x^17/n!(17) - x^19/n!(19) + x^21/n!(21) - x^23/n!(23) + x^25/n!(25) - x^27/n!(27) + x^29/n!(29) ) * ( x - x^03/n!(03) + x^05/n!(05) - x^07/n!(07) + x^09/n!(09) - x^11/n!(11) + x^13/n!(13) - x^15/n!(15) + x^17/n!(17) - x^19/n!(19) + x^21/n!(21) - x^23/n!(23) + x^25/n!(25) - x^27/n!(27) + x^29/n!(29) ) * ( x - x^03/n!(03) + x^05/n!(05) - x^07/n!(07) + x^09/n!(09) - x^11/n!(11) + x^13/n!(13) - x^15/n!(15) + x^17/n!(17) - x^19/n!(19) + x^21/n!(21) - x^23/n!(23) + x^25/n!(25) - x^27/n!(27) + x^29/n!(29) ) * ( x - x^03/n!(03) + x^05/n!(05) - x^07/n!(07) + x^09/n!(09) - x^11/n!(11) + x^13/n!(13) - x^15/n!(15) + x^17/n!(17) - x^19/n!(19) + x^21/n!(21) - x^23/n!(23) + x^25/n!(25) - x^27/n!(27) + x^29/n!(29) ) * ( x - x^03/n!(03) + x^05/n!(05) - x^07/n!(07) + x^09/n!(09) - x^11/n!(11) + x^13/n!(13) - x^15/n!(15) + x^17/n!(17) - x^19/n!(19) + x^21/n!(21) - x^23/n!(23) + x^25/n!(25) - x^27/n!(27) + x^29/n!(29) ) * ( x - x^03/n!(03) + x^05/n!(05) - x^07/n!(07) + x^09/n!(09) - x^11/n!(11) + x^13/n!(13) - x^15/n!(15) + x^17/n!(17) - x^19/n!(19) + x^21/n!(21) - x^23/n!(23) + x^25/n!(25) - x^27/n!(27) + x^29/n!(29) ) * ( x - x^03/n!(03) + x^05/n!(05) - x^07/n!(07) + x^09/n!(09) - x^11/n!(11) + x^13/n!(13) - x^15/n!(15) + x^17/n!(17) - x^19/n!(19) + x^21/n!(21) - x^23/n!(23) + x^25/n!(25) - x^27/n!(27) + x^29/n!(29) ) * ( x - x^03/n!(03) + x^05/n!(05) - x^07/n!(07) + x^09/n!(09) - x^11/n!(11) + x^13/n!(13) - x^15/n!(15) + x^17/n!(17) - x^19/n!(19) + x^21/n!(21) - x^23/n!(23) + x^25/n!(25) - x^27/n!(27) + x^29/n!(29) ) * ( x - x^03/n!(03) + x^05/n!(05) - x^07/n!(07) + x^09/n!(09) - x^11/n!(11) + x^13/n!(13) - x^15/n!(15) + x^17/n!(17) - x^19/n!(19) + x^21/n!(21) - x^23/n!(23) + x^25/n!(25) - x^27/n!(27) + x^29/n!(29) ) * ( x - x^03/n!(03) + x^05/n!(05) - x^07/n!(07) + x^09/n!(09) - x^11/n!(11) + x^13/n!(13) - x^15/n!(15) + x^17/n!(17) - x^19/n!(19) + x^21/n!(21) - x^23/n!(23) + x^25/n!(25) - x^27/n!(27) + x^29/n!(29) ) * ( x - x^03/n!(03) + x^05/n!(05) - x^07/n!(07) + x^09/n!(09) - x^11/n!(11) + x^13/n!(13) - x^15/n!(15) + x^17/n!(17) - x^19/n!(19) + x^21/n!(21) - x^23/n!(23) + x^25/n!(25) - x^27/n!(27) + x^29/n!(29) ) * ( x - x^03/n!(03) + x^05/n!(05) - x^07/n!(07) + x^09/n!(09) - x^11/n!(11) + x^13/n!(13) - x^15/n!(15) + x^17/n!(17) - x^19/n!(19) + x^21/n!(21) - x^23/n!(23) + x^25/n!(25) - x^27/n!(27) + x^29/n!(29) ) Als Definitionsbereich wird xl = -6 und xr = 6 empfohlen. Achtung: Die Formellänge (ohne Leerzeichen) beträgt über 7700 Zeichen und kann aufgrund des hohen Rechenaufwandes durchaus 20 Sekunden bis zur Plotausgabe benötigen! Empfehlung: Geben Sie in der Eingabemaske für f 1 den Term sin(x)^35 ein und übertragen Sie die obige (grüne) Formel komplett mittels „Kopieren und Einfügen“ in den Eingabe- bereich f 2 . Die Eingabebereiche f 3 und f 4 können Sie, falls diese nicht leer sind, durch jeweils einen Maus-Doppelklick löschen. Wie das Ergebnis der Berechnung zeigt, konvergiert die Näherung sehr langsam, erkennbar an den nicht absolut deckungsgleich verlaufenden Kurven f 1 (rot) und f 2 (blau). Anmerkung: Der wesentlicher Zeitanteil liegt in der Konvertierung der Formel. Die Anzahl der anschließenden Berechnungen sind zeitlich untergeordnet.