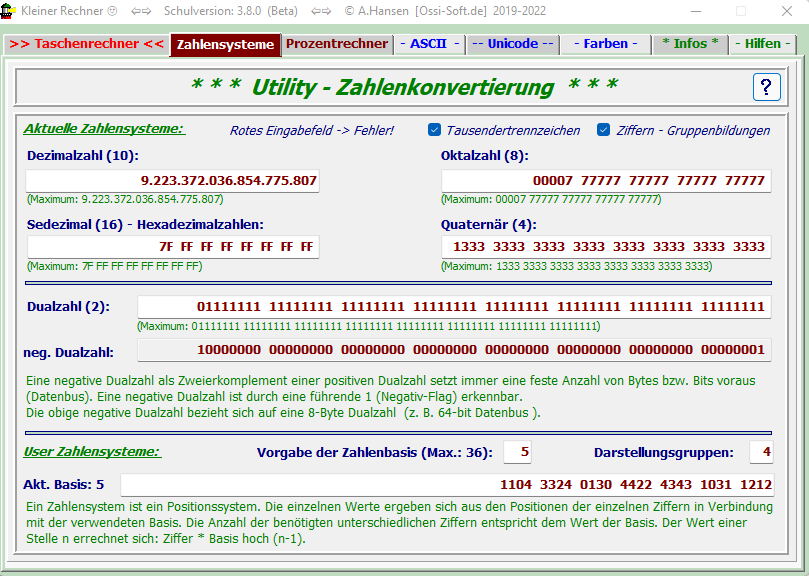
Ein Zahlensystem ist ein Positionssystem. Die einzelnen Werte ergeben sich aus den Positionen der einzelnen Ziffern in Verbindung mit der verwendeten Basis. Die Anzahl der benötigten unterschiedlichen Ziffern entspricht dem Wert der Basis, also mit der Basis = 8 werden 8 Ziffern (0-7) benötigt. Der Wert einer Stelle n errechnet sich: n-te Ziffer * Basis hoch n, wobei die letzte Ziffer einer ganzen Zahl die Position 0, also n=0, hat. Allgemein gilt für Zahlen ohne Kommata (B=Basis, n=Anzahl der Positionen - 1): Beispiele: 345.678 (10) = 3 * 10 5 + 4 * 10 4 + 5 * 10 3 + 6 * 10 2 + 7 * 10 1 + 8 * 10 0 also 345.678 (10) = 3 * 100000 + 4 * 10000 + 5 * 10000 + 6 * 100 + 7 * 10 + 8 * 1 765432 (8) = 7 * 8 5 + 6 * 8 4 + 5 * 8 3 + 4 * 8 2 + 3 * 8 1 + 2 * 8 0 also 765432 (8) = 7 * 32768 + 6 * 4096 + 5 * 512 + 4 * 64 + 3 * 8 + 2 * 1 Das Utility „Zahlenkonvertierungen“ ist auch als ein komfortables Hilfsmittel für EDV - Anwendungen, z: B. Analysen auf Bitebene von Texten, Steuersequenzen, Konvertierungen, Kennungen usw., zu sehen. Auch direkt in der Informatik bzw. Mathematik ist es ein oft benötigtes Hilfsmittel. Im Bereich „Zahlenkonvertierung“ können Zahlen von einem beliebigen Zahlensystem in ein anderes beliebiges Zahlensystem konvertiert werden. 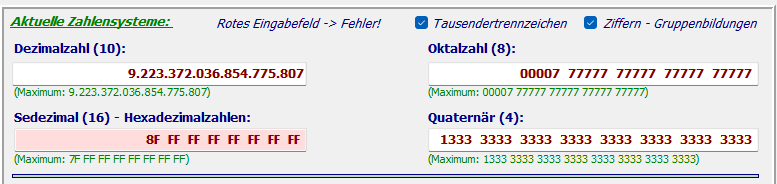Der Zahlenraum umfasst den Dezimalbereich von 0 bis 9.223.372.036.854.775.807, gleichbedeutend z: B. im Hex-Bereich von 0 bis 7F FF FF FF FF FF FF FF. Die wählbaren Basen für die Zahlensysteme wurden auf den Zahlenraum von 2 bis 36 begrenzt. Die Konvertierung wird in einem Zahleneingabefeld, in dem sich die zu konvertierende Zahl befindet bzw. eingegeben wurde, durch Betätigung der „Enter-Taste“ (Knickpfeiltaste) eingeleitet. Ausnahme: Im Zahlenfeld „neg. Dualzahl“ ist keine Eingabe möglich. 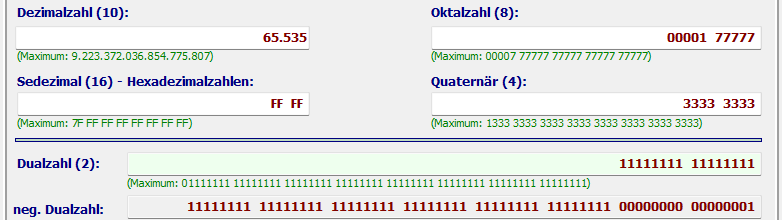Im Datenfeld „neg. Dualzahl“ wird das Zweierkomplement der oberhalb stehenden 8-Byte Dualzahl ausgegeben. 8-Byte Dualzahlen können den Signalzustand auf einen 64-Bit Datenbus (EDV) wiedergeben bzw. beschreiben (Assembler-Programmierung usw.). 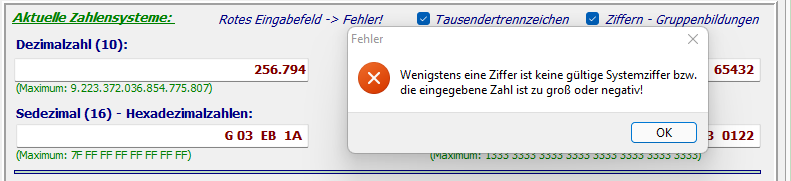Hinweis: Ein rot gefärbtes Eingabefeld weist auf eine fehlerhafte Eingabe hin. Eine Konvertierung hat dann nicht stattgefunden. Dieses gilt auch für Fehlermeldungen! 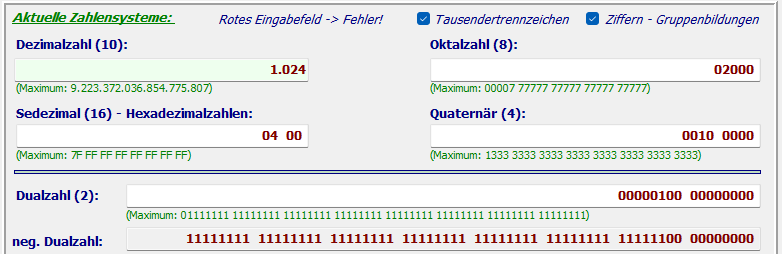Dezimalzahl 1024 (Entertaste) Ergebnisse: Hexzahl = 04 00 und Oktalzahl = 2000 usw. 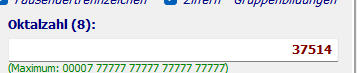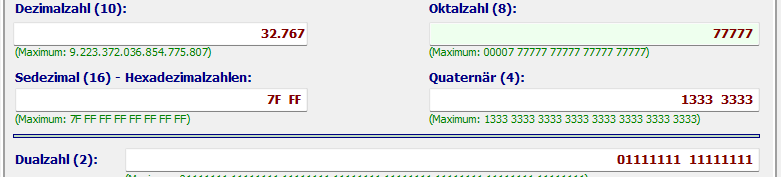Oktalzahl 77777 (Entertaste) Ergebnisse: Hexzahl = 7F FF und Dezimalzahl = 32.767 usw. 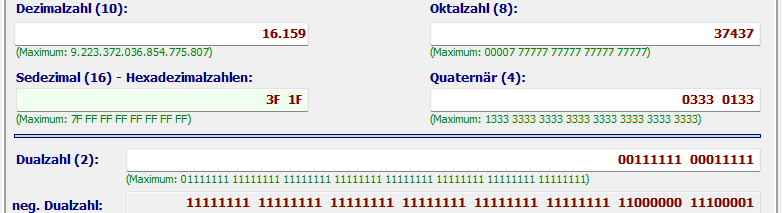Hex Zahl 3F1F (Entertaste) Ergebnisse: Dezimalzahl = 16.159 usw. 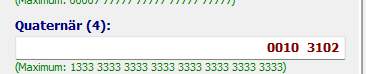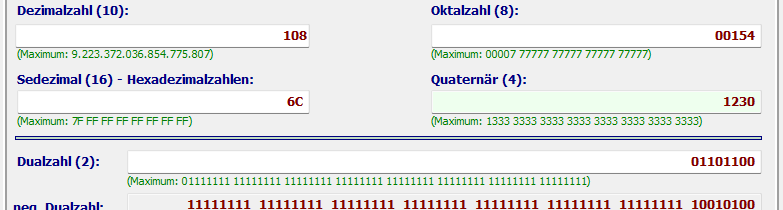Quaternär 1230 (Entertaste) Ergebnisse: Hexzahl = 6C und Dezimalzahl = 108 usw. Dualzahl 11111111 11111111 (Entertaste) Ergebnisse: Hexzahl = FF FF und Dezimalzahl = 65.535 usw. Dieses offene Zahlensystem erlaubt sowohl die Konvertierung als auch die Anzeige von Zahlen mit wählbaren Basen, die in gewünschter Gruppierung ausgegeben werden können. Jede mit der Entertaste durchgeführte Änderung führt zur Aktualisierung der Ausgaben. Die Darstellungsgruppenlängen sind (sinnvollerweise) auf 16 begrenzt. Bei der Länge 0 erfolgt keine Gruppierung. Die (sinnvollerweise vorgegebene) maximale Größe der Basis beträgt 36. Hierfür wird dann der Ziffernvorrat von [ 0, 1, 2, … , 8, 9, A, B, C, ..., X, Y, Z ] benötigt, also 36 Ziffern. Die ganz allgemeine Konvertierungen von Zahlen aus ungewöhnlichen Zahlensystemen in andere (ungewöhnliche) Zahlensysteme verläuft im Abschnitt „User – Zahlensysteme“ immer nach dem Muster: 1. Eingabe der ersten Ausgangszahlenbasis (Enter). 2. Eingabe der zugehörigen Ziffernfolge (Zahl) (Enter). 3. Eingabe der neuen Zahlenbasis. Die Entertaste leitet die Konvertierung der aktuellen Zahl in das gewünschte Zahlensystem ein. Konvertierung der Zahl 1234 zur Basis 12 in eine Zahl zur Basis 28: Ergebnisse: (142) 12 = (6Q) 28 Konvertierung der Zahl 21 3043 2104 4103 2200 1123 zur Basis 5 in eine Zahl zur Basis 36: Ergebnisse: (21 3043 2104 4103 2200 1123) 5 = (AXEL HANSEN) 36 Anmerkung: Hier sind auch Gruppierungsänderungen von Zahlensystemen möglich. 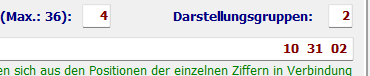Beispiele Gruppierungsänderungen: 1. 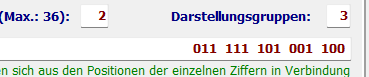Zweiergruppierung im 4er-System: => Änderungen: Zahlenbasis: 4; Darstellungsgruppen: 2 ➪ 2. Dreiergruppierung im 2er-System: => Änderungen: Zahlenbasis: 2; Darstellungsgruppen: 3 ➪ Anmerkung: Mittels Gruppierungen lassen sich auch übersichtlich die Eigenschaften von Zahlen- systemen zeigen. Ziffern - Oktal: 3 7 5 1 4 Ziffern - Dual: 011 111 101 001 100