Beispiel: Tief- und Hochpass
Beispiel: Tief- und Hochpass

Anwendungsbereich: Filterschaltungen
Anwendungsbereich: Filterschaltungen




Beispiel: LC - Bandpass
Beispiel: LC - Bandpass

Anwendungsbereich: Filterschaltungen
Anwendungsbereich: Filterschaltungen







Beispiel: LC - Bandsperre
Beispiel: LC - Bandsperre

Anwendungsbereich: Filterschaltungen
Anwendungsbereich: Filterschaltungen






Exponentialform: Beispiel LC - Bandpass
Exponentialform: Beispiel LC - Bandpass

Anwendungsbereich: Filterschaltungen
Anwendungsbereich: Filterschaltungen
Kartesische (arithmetische) Form - Polarform (Exponentialform)
Kartesische (arithmetische) Form - Polarform (Exponentialform)
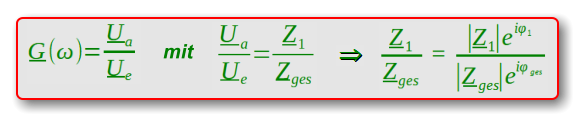



Die hier gezeigten exemplarischen Beispiele demonstrieren nicht nur den universellen Rechner-
einsatz, sondern zeigen auch modifizierbare Lösungsstrategien im Umgang mit komplexen
Schaltungen.
Eingabehinweis: Ein Doppelklick im Eingabefenster löscht die akt. Eingabe.
Die in den Beispielen entwickelten Formeln und Funktionen können direkt in die Eingabebereiche des
„Kleinen Rechners“ kopiert werden (copy and paste). Bei Funktionsgleichungen wird der linke Teil incl.
Gleichheitszeichen ignoriert.
Winkelein- und Ausgaben können auf drei Arten erfolgen (Bogenmaß, Altgrad, Neugrad;
siehe Hauptmaske „Taschenrechner“).
Da in der Elektrotechnik in Verbindung mit Phasengängen usw. oft im „Altgrad-
modus“ gerechnet wird, wählen Sie bitte in der Hauptmaske die Option
Winkeleinstellung „Grad“!
Um eine erstellte komplexe Formeln bezüglich der elektrischen Werte schnell variieren zu können,
werden gerne Parameter (Platzhalter) innerhalb der Formeln verwendet.
In Schaltungen werden z. B. oft mehrere Widerstände, Kondensatoren und Induktivitäten
verwendet. Hier könnte es vorteilhaft sein, allgemein über eine (eigene) Verwendungsordnung
nachzudenken.
In den Beispielen werden meistens für ohmsche Widerstände R die Parameter „R“ und „W“ und
bei Bedarf auch „U“ und „V“ , für elektrische Induktivitäten L die Parameter „L“ und „B“ und für
elektrische Kapazitäten C die Parameter „C“ und „A“ verwendet.
Beispiel: Verlustbehafteter Parallelschwingkreis:
|Z Parallel (x)| = { [( { [ 1 / W ] / [ 1/W^2 + { 2*Pi*x*C - 1/(2*Pi*x*L) }^2 ] } )^2] +
[( { [ 1 / (2*Pi*x*L) - 2*Pi*x*C ] / [ 1/W^2 + { 2*Pi*x*C - 1/(2*Pi*x*L) }^2 ] } )^2] }^0,5
Zugehörige Beispielparameterliste:
Empfehlung: Löschen Sie vor der Eingabe die Parameterliste (Doppelklick auf Mülltonne). Falls Sie
dann einen Parameter vergessen (oder fehlerhaft eingegeben) haben, erscheint nach
einer Plotausgabe in der Parameterliste ein Fehlerhinweis (????)!
Hier wurde kein Parameter eingetragen! Angezeigt werden alle verwendeten Parameter.
Falls mehrere Kurven mit großen unterschiedlichen Wertebereichen übersichtlich in einem
Koordinatensystem dargestellt werden sollen, ist es oft notwendig, Kurven dementsprechend zu
skalieren.
Dieses gilt hier oft für den Phasengang φ(f) mit φ(f)∈[ -180°; 180° ], der dem Ausgabewertebereich
Y ∈ [ -0,2; 1,2] angepasst werden soll. Hier ist eine Stauchung mit dem Faktor 0,001 notwendig.
f: x→f = c * ( φ(x) ); mit c=0,001 gilt: f: x→f = 0,001 * ( φ(x) ) Fehlerquelle: gesamten Term klammern!
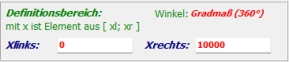
Die verwendeten Frequenzbereiche liegen i. Allg. zwischen 0 Hz
und 10 kHz. Sie werden jeweils im Definitionsbereich eingestellt.
(Entnehmen Sie hier die aktuellen Werte aus den Plotdarstellungen.)
Der Wertebereich kann jederzeit im Ausgabefenster in Echtzeit angepasst werden.
(Entnehmen Sie hier die aktuellen Werte aus den Plotdarstellungen.)
Parameterverwendungen:
Parameterverwendungen:


Funktionsgraphen skalieren (y-Achse):
Funktionsgraphen skalieren (y-Achse):
Abzisse (x-Achse):
Abzisse (x-Achse):
Hinweise für die hier vorgestellten Beispiele
Hinweise für die hier vorgestellten Beispiele

Winkelmodus:
Winkelmodus:


Ordinate (y-Achse):
Ordinate (y-Achse):

Passive Filter bestehen aus der Kombination von passiven Bauteilen wie z. B. Kondensatoren,
Spulen und Widerstände.
Grob formuliert gilt:
Tiefpassfilter lassen Wechselspannungen bis zu ihrer Grenzfrequenz passieren,
Hochpassfilter lassen Wechselspannungen ab ihrer Grenzfrequenz passieren.
Es werden hier die Eigenschaften von unbelasteten Filtern untersucht. Innenwiderstände von
Signalquellen sowie die Abschluss- bzw. Eingangswiderstände etwaiger Folgestufen werden hier
nicht berücksichtigt.
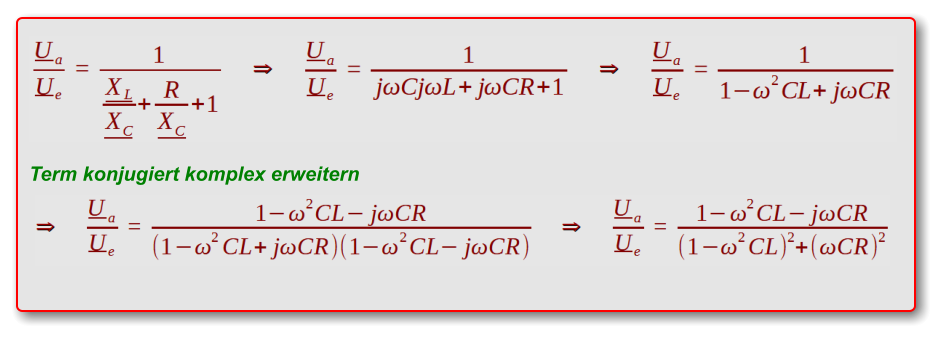
Exemplarisch wird hier der Spannungsverlauf der Ausgangsspannung U
a
am Kondensator im
Verhältnis zur Eingangsspannung U
e
in Abhängigkeit der Frequenz ermittelt.
Auch im komplexen Bereich gilt das 2. Kirchhoffsches Gesetz (Maschenregel) ∑ U = 0
In einer Reihenschaltung ist der fließende Strom in allen
Widerständen gleich.
Formel in Real- und Imaginärteil splitten:
Variable x = f (ω = 2ℼf), Parameter L = L [H]; C = C [F]; R = R [Ω]
Nenner: { [1-( 2*Pi*x)^2*C*L ]^2 + [ 2*Pi*x*C*R ]^2 }
f
1
: |Z(x)| = {[( { [ 1-(2*Pi*x)^2*C*L ] / { [1-( 2*Pi*x)^2*C*L ]^2 + [ 2*Pi*x*C*R ]^2 } } )^2] +[(
{ [ -2*Pi*x*C*R ] / { [1-( 2*Pi*x)^2*C*L ]^2 + [ 2*Pi*x*C*R ]^2 } } )^2]}^0,5
φ(x) = arctan[ ( { [ -2*Pi*x*C*R ] / { [1-( 2*Pi*x)^2*C*L ]^2 + [ 2*Pi*x*C*R ]^2 } } ) / (
{ [ 1-(2*Pi*x)^2*C*L ] / { [1-( 2*Pi*x)^2*C*L ]^2 + [ 2*Pi*x*C*R ]^2 } } ) ]
Zur Darstellung des Phasengangs wird die Funktion φ gestaucht: φ*: x → φ*(x) = 0,001 * { φ(x) }.
f
2
: φ*(x) = 0,001 * { arctan[ ( { [ -2*Pi*x*C*R ] / { [1-( 2*Pi*x)^2*C*L ]^2 + [ 2*Pi*x*C*R ]^2 } } ) / (
{ [ 1-(2*Pi*x)^2*C*L ] / { [1-( 2*Pi*x)^2*C*L ]^2 + [ 2*Pi*x*C*R ]^2 } } ) ] }
Um die Abhängigkeit der Übertragungsfunktion von dem Widerstandswert R übersichtlich
darstellen zu können, sollen drei im Widerstandswert veränderbare unabhängige Kurven (rot,
grün, magenta) dargestellt werden können. Hierfür werden zwei Kopien der Übertragungsfunktion
erstellt und der Widerstand R durch die Parameter V und W ersetzt.
f
3
: |Z(x)| = {[( { [ 1-(2*Pi*x)^2*C*L ] / { [1-( 2*Pi*x)^2*C*L ]^2 + [ 2*Pi*x*C*V ]^2 } } )^2] + [(
{ [ -2*Pi*x*C*V ] / { [1-( 2*Pi*x)^2*C*L ]^2 + [ 2*Pi*x*C*V ]^2 } } )^2]}^0,5
f
4
: |Z(x)| = {[( { [ 1-(2*Pi*x)^2*C*L ] / { [1-( 2*Pi*x)^2*C*L ]^2 + [ 2*Pi*x*C*W ]^2 } } )^2] + [(
{ [ -2*Pi*x*C*W ] / { [1-( 2*Pi*x)^2*C*L ]^2 + [ 2*Pi*x*C*W ]^2 } } )^2]}^0,5
Werte:
X
L
: L = 10 mH (10e-3 H ) → L = 1eE-3; X
C
: C = 100 nF (100e-9 F) → C = 100E-9;
Parameter R:
R = 470 Ω (rot, blau)
→ R = 470;
R = 300 Ω (grün);
→ V = 300;
R = 5000 Ω (magenta);
→ W = 5000;
Winkelmodus: Gradmaß (360°); Phasengang ist gestaucht → - 0,90° ≤ 0,001 * [ φ*(f) ] ≤ 0,90°
⇒ Der zulässige Widerstandsbereich (R) ist abhängig von der LC-Kombination. ⇐
Die Übertragungsfunktion G(ω) dieses Filter (Reihenschwingkreis) wurde bereits
im Abschnitt Spannungsüberhöhungen indirekt berechnet.
Formelerstellung: siehe Abschnitt „Spannungsüberhöhungen“ im Reihenschwingkreis.
f
1
: |Z(x)| = {[( [ 1-1/[(2*Pi*x)^2*C*L] ] / [ { 1-1/[ (2*Pi*x)^2*C*L ] }^2 + { R /[2*Pi*x*L] }^2 ] )^2] + [(
[ R /(2*Pi*x*L) ] / [ { 1-1/[ (2*Pi*x)^2*C*L ] }^2 + { R /[2*Pi*x*L] }^2 ] )^2]}^0,5
φ(x) = arctan[ ( [ R /(2*Pi*x*L) ] / [ { 1-1/[ (2*Pi*x)^2*C*L ] }^2 + { R /[2*Pi*x*L] }^2 ] ) / (
[ 1-1/[(2*Pi*x)^2*C*L] ] / [ { 1-1/[ (2*Pi*x)^2*C*L ] }^2 + { R /[2*Pi*x*L] }^2 ] ) ]
Anmerkung: Phasengang gestaucht f
2
: φ*(x) = c * ( φ(x) ); hier: c = 0,001
f
2
: φ*(x) = 0,001 * { arctan[ ( [ R/(2*Pi*x*L) ] / [ { 1-1/[ (2*Pi*x)^2*C*L ] }^2 + { R/[2*Pi*x*L] }^2 ] ) / (
[ 1-1/[(2*Pi*x)^2*C*L] ] / [ { 1-1/[ (2*Pi*x)^2*C*L ] }^2 + { R/[2*Pi*x*L] }^2 ] ) ] }
_______________________
f
3
: |Z(x)| = {[( [ 1-1/[(2*Pi*x)^2*C*L] ] / [ { 1-1/[ (2*Pi*x)^2*C*L ] }^2 + { V /[2*Pi*x*L] }^2 ] )^2] + [(
[ V /(2*Pi*x*L) ] / [ { 1-1/[ (2*Pi*x)^2*C*L ] }^2 + { V /[2*Pi*x*L] }^2 ] )^2]}^0,5
f
4
: |Z(x)| = {[( [ 1-1/[(2*Pi*x)^2*C*L] ] / [ { 1-1/[ (2*Pi*x)^2*C*L ] }^2 + { W /[2*Pi*x*L] }^2 ] )^2] + [(
[ W /(2*Pi*x*L) ] / [ { 1-1/[ (2*Pi*x)^2*C*L ] }^2 + { W /[2*Pi*x*L] }^2 ] )^2]}^0,5
Werte:
X
L
: L = 10 mH (10e-3 H ) → L = 1eE-3; X
C
: C = 100 nF (100e-9 F) → C = 100E-9;
Parameter R:
R = 470 Ω (rot, blau)
→ R = 470;
R = 300 Ω (grün);
→ V = 300;
R = 5 kΩ (magenta);
→ W = 5000;
Winkelmodus: Gradmaß (360°)
Die magentafarbige Kurve nähert sich asymtotisch der Geraden y=1 (Ansicht z. B. f ∈ [0;100kHz])
_______________________________________________
Anregung: Wie durch die passende Veränderung der Parameter C, L und R gezeigt werden kann, zum Beispiel
in der Kombination L
2
=100 mH, C
2
=10 nF (L
1
* C
1
= L
2
* C
2
) und R
2
= 4,7 kΩ, generieren diese
Werte ebenfalls die obige rote Übertragungskurve.
Probieren Sie:
Parameter für die Funktionsgleichungen f
1
und f
2
: R → R; C → C; L → L;
Parameter für die Funktionsgleichungen f
3
und f
4
: R → W; C → A; L → B;
f
1
: |Z(x)| = {[( [ 1-1/[(2*Pi*x)^2*C*L] ] / [ { 1-1/[ (2*Pi*x)^2*C* L ] }^2 + { R /[2*Pi*x*L] }^2 ] )^2] +
[( [ R /(2*Pi*x*L) ] / [ { 1-1/[ (2*Pi*x)^2*C* L ] }^2 + { R /[2*Pi*x*L] }^2 ] )^2]}^0,5
f
3
: |Z(x)| = {[( [ 1-1/[(2*Pi*x)^2*A*B] ] / [ { 1-1/[ (2*Pi*x)^2*A* B ] }^2 + { W /[2*Pi*x*B] }^2 ] )^2] +
[( [ W /(2*Pi*x*B) ] / [ { 1-1/[ (2*Pi*x)^2*A* B ] }^2 + { W /[2*Pi*x*B] }^2 ] )^2]}^0,5
f
2
: φ*(x) = 0,001 * { arctan[ ( [ R/(2*Pi*x* L) ] / [ { 1-1/[ (2*Pi*x)^2*C* L ] }^2 + { R/[2*Pi*x*L] }^2 ] ) /
( [ 1-1/[(2*Pi*x)^2*C*L] ] / [ { 1-1/[ (2*Pi*x)^2*C* L ] }^2 + { R/[2*Pi*x*L] }^2 ] ) ] }
f
4
: φ*(x) = 0,001 * { arctan[ ( [ W/(2*Pi*x*B) ] / [ { 1-1/[ (2*Pi*x)^2*A* B ] }^2 + { W/[2*Pi*x*B] }^2 ] ) /
( [ 1-1/[(2*Pi*x)^2*A*B] ] / [ { 1-1/[ (2*Pi*x)^2*A* B ] }^2 + { W/[2*Pi*x*B] }^2 ] ) ] }
Beispiel: R = 470; C = 100E-9; L = 10E-3; W = 4700; A = 10E-9; B = 100E-3
(Verwenden Sie im Plotfenster den Modus „Full Screen“ und schalten Sie temporär f
3
und f
4
aus)
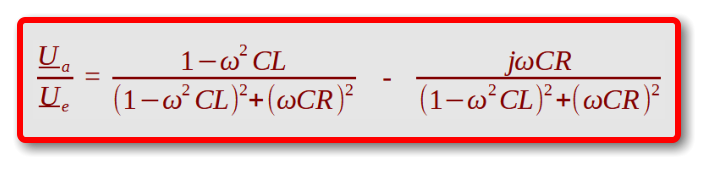


U
e
U
a
X
C
X
L
R
Formelumsetzungen für Plotausgaben
Formelumsetzungen für Plotausgaben
Bezeichnungen:
Bezeichnungen:
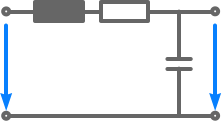
Ansatz:
Ansatz:
Formelerstellung:
Formelerstellung:

U
L
+ U
R
+ U
a
- U
e
= 0 ⇒ U
e
= U
L
+ U
R
+ U
a
Berechnungen:
Berechnungen:
Tiefpassfilter:
Tiefpassfilter:

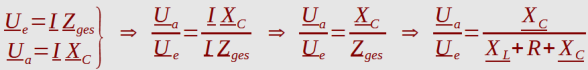
Hochpassfilter:
Hochpassfilter:

U
a
U
e

X
C
X
L
R

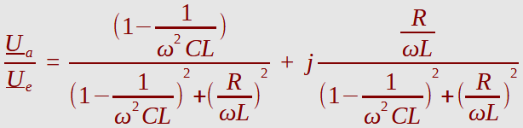

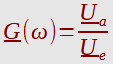
Formelumsetzungen für Plotausgaben
Formelumsetzungen für Plotausgaben
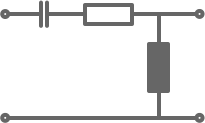
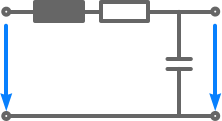
Schaltung und Formel:
Schaltung und Formel:


U
e
U
a
X
C
X
L
R

Realteil
= { [ 1-(2*Pi*x)^2*C*L ] / { [1-( 2*Pi*x)^2*C*L ]^2 + [ 2*Pi*x*C*R ]^2 } }
Imaginärteil
= { [ -2*Pi*x*C*R ] / { [1-( 2*Pi*x)^2*C*L ]^2 + [ 2*Pi*x*C*R ]^2 } }

Realteil
= [ 1-1/[(2*Pi*x)^2*C*L] ] / [ { 1-1/[ (2*Pi*x)^2*C*L ] }^2 + { R/[2*Pi*x*L] }^2 ]
Imaginärteil
= [ R/(2*Pi*x*L) ] / [ { 1-1/[ (2*Pi*x)^2*C*L ] }^2 + { R/[2*Pi*x*L] }^2 ]
Filterschaltungen (aktive und passive) sperren bestimmte Frequenzbereiche aus einem breiten
Frequenzgemisch oder lassen diese durch.
Ein Bandpass überträgt ein nach unten und oben begrenztes Frequenzband (f
L
-f
0
-f
H
).
Eine Bandsperre sperrt ein nach unten und oben begrenztes Frequenzband.
Bandsperren, auch Bandstopp Filter genannt, sperren die Übertragung eines vorgegebenen
Frequenzbereichs (Frequenzband).
Passive Bandsperren bestehen nur aus passiven Bauelementen.
Ausgehend von den Formeln für idealen Parallel- und realen Reihen-
schwingkreise wird die Übertragungsfunktion erstellt.
Da u. a. der Funktionsgraf dieser Funktion vom Programm „Kleiner
Rechner“ geplottet werden soll - hier spielt die Formellänge keine
wesentliche Rolle - ist es nicht Ziel, eine bis ins Kleinste optimierte
(fehlerträchtige) Formel zu erstellen.
Übertragungsfunktion
Idealer Parallelschwingkreis
Realer Reihenschwingkreis:
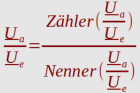
Da der Hauptnenner der obigen Übertragungsfunktion real ist, kann der komplexe Zähler getrennt
weiter umgeformt werden. Die Zusammenführung erfolgt nach der Zerlegung des Zählers in seine
real- und Imaginärteile.
Neben der Variablen x, x = f sollen nachfolgende Parameter verwendet
werden.
Parallelschwingkreis (Z
1
):
C = C
1
[F]; L = L
1
[H];
Reihenschwingkreis (Z
2
):
A = C
2
[F]; B = L
2
[H]; R = R [Ω]
____________________
Nenner
= { R^2 + ( 2*Pi*x*L / (1-(2*Pi*x)^2*L*C ) + 2*Pi*x*B - 1/(2*Pi*x*A) )^2 }
Re(Zähler)
= { R^2 + [ 2*Pi*x*B -1/(2*Pi*x*A) ]*[ 2*Pi*x*L/(1-(2*Pi*x)^2*L*C) + 2*Pi*x*B - 1/(2*Pi*x*A) ] }
Im(Zähler)
= { 2*Pi*x*R*L / ( (2*Pi*x)^2*L*C-1 ) }
Hieraus ergibt sich für den Real- und dem Imaginärteil der Übertragungsfunktion:
Der Real- und der Imaginärteil werden in die Formelgerüste eingesetzt und ergeben die direkt kopierbaren
Formeln.
|Z(x)| = {[( Re )^2] + [( Im )^2]}^0,5
φ(x) = arctan[ ( Im ) / ( Re ) ] (mit Re ≠ 0; Winkeleinstellung: Altgrad 360°)
f
1
: |Z(x)| = {[( { R^2 + [ 2*Pi*x*B -1/(2*Pi*x*A) ]*[ 2*Pi*x*L/(1-(2*Pi*x)^2*L*C) + 2*Pi*x*B - 1/(2*Pi*x*A) ] } /
{ R^2 + ( 2*Pi*x*L / (1-(2*Pi*x)^2*L*C ) + 2*Pi*x*B - 1/(2*Pi*x*A) )^2 } )^2] + [(
{ 2*Pi*x*R*L / ( (2*Pi*x)^2*L*C-1 ) } /
{ R^2 + ( 2*Pi*x*L / (1-(2*Pi*x)^2*L*C ) + 2*Pi*x*B - 1/(2*Pi*x*A) )^2 } )^2]}^0,5
φ(x) = arctan[ ( { 2*Pi*x*R*L / ( (2*Pi*x)^2*L*C-1 ) } / { R^2 + ( 2*Pi*x*L / (1-(2*Pi*x)^2*L*C ) + 2*Pi*x*B - 1/(2*Pi*x*A) )^2 } ) / (
{ R^2 + [ 2*Pi*x*B -1/(2*Pi*x*A) ]*[ 2*Pi*x*L/(1-(2*Pi*x)^2*L*C) + 2*Pi*x*B - 1/(2*Pi*x*A) ] } /
{ R^2 + ( 2*Pi*x*L / (1-(2*Pi*x)^2*L*C ) + 2*Pi*x*B - 1/(2*Pi*x*A) )^2 } ) ]
Der Phasengang wird gestaucht, Stauchungsfaktor = 0,005:
f
2
: φ*(x) = 0,005 * { arctan[ ( { 2*Pi*x*R*L / ( (2*Pi*x)^2*L*C-1 ) } / { R^2 + ( 2*Pi*x*L / (1-(2*Pi*x)^2*L*C ) + 2*Pi*x*B -
1/(2*Pi*x*A) )^2 } ) / ( { R^2 + [ 2*Pi*x*B -1/(2*Pi*x*A) ]*[ 2*Pi*x*L/(1-(2*Pi*x)^2*L*C) + 2*Pi*x*B -
1/(2*Pi*x*A) ] } / { R^2 + ( 2*Pi*x*L / (1-(2*Pi*x)^2*L*C ) + 2*Pi*x*B - 1/(2*Pi*x*A) )^2 } ) ] }
f
3
: 3dB-Grenze = 0,708
Werte: X
L1
: L
1
= 10 mH → L = 10E-3; X
C1
: C
1
= 100 nF → C = 100E-9;
X
L2
: L
2
= 10 mH
→ B = 10E-3,
X
C2
: C
2
= 100 nF
→ A = 100E-9; R = 4,7 kΩ → R = 4700
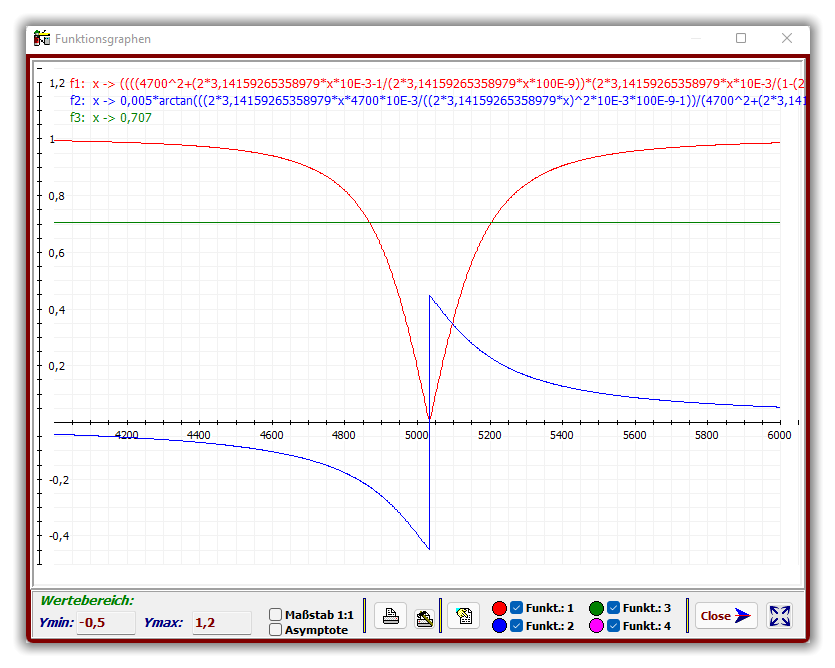
Die obigen Kurvenverläufe zeigen eine Bandsperre mit der Sperrfrequenz f
0
= 5033 Hz und einer
Bandbreite (- 3 db) von ca. 340 Hz mit den Grenzfrequenzen f
L
≈ 4870 Hz und f
H
≈ 5205 Hz.
Zur Erstellung der Funktionsgleichungen wird die obige Funktionsgleichung f
1
modifiziert.
f
2
: |Z(x)| = {[( { U^2 + [ 2*Pi*x*B -1/(2*Pi*x*A) ]*[ 2*Pi*x*L/(1-(2*Pi*x)^2*L*C) + 2*Pi*x*B - 1/(2*Pi*x*A) ] } /
{ U^2 + ( 2*Pi*x*L / (1-(2*Pi*x)^2*L*C ) + 2*Pi*x*B - 1/(2*Pi*x*A) )^2 } )^2] + [(
{ 2*Pi*x*U*L / ( (2*Pi*x)^2*L*C-1 ) } /
{ U^2 + ( 2*Pi*x*L / (1-(2*Pi*x)^2*L*C ) + 2*Pi*x*B - 1/(2*Pi*x*A) )^2 } )^2]}^0,5
f
3
: |Z(x)| = {[( { V^2 + [ 2*Pi*x*B -1/(2*Pi*x*A) ]*[ 2*Pi*x*L/(1-(2*Pi*x)^2*L*C) + 2*Pi*x*B - 1/(2*Pi*x*A) ] } /
{ V^2 + ( 2*Pi*x*L / (1-(2*Pi*x)^2*L*C ) + 2*Pi*x*B - 1/(2*Pi*x*A) )^2 } )^2] + [(
{ 2*Pi*x*V*L / ( (2*Pi*x)^2*L*C-1 ) } /
{ V^2 + ( 2*Pi*x*L / (1-(2*Pi*x)^2*L*C ) + 2*Pi*x*B - 1/(2*Pi*x*A) )^2 } )^2]}^0,5
f
4
: |Z(x)| = {[( { W^2 + [ 2*Pi*x*B -1/(2*Pi*x*A) ]*[ 2*Pi*x*L/(1-(2*Pi*x)^2*L*C) + 2*Pi*x*B - 1/(2*Pi*x*A) ] } /
{ W^2 + ( 2*Pi*x*L / (1-(2*Pi*x)^2*L*C ) + 2*Pi*x*B - 1/(2*Pi*x*A) )^2 } )^2] + [(
{ 2*Pi*x*W*L / ( (2*Pi*x)^2*L*C-1 ) } /
{ W^2 + ( 2*Pi*x*L / (1-(2*Pi*x)^2*L*C ) + 2*Pi*x*B - 1/(2*Pi*x*A) )^2 } )^2]}^0,5
Werte:
Paralleschwingkreis:
X
L1
: L
1
= 10 mH → L = 10E-3; X
C1
: C
1
= 100 nF → C = 100E-9;
Reihenschingkreis:
X
L2
: L = 10 mH → B = 10E-3, X
C2
: C
2
= 100 nF → A = 100E-9;
Für den Widerstand R wurden die nachfolgenden Parameter verwendet:
R
r
(rot) = 4,7 kΩ
→ R = 4700;
R
b
(blau) = 270 Ω → U = 270;
R
g
(grün) = 1 kΩ
→ V = 1000; R
m
(magenta) = 15 kΩ → W = 15000;
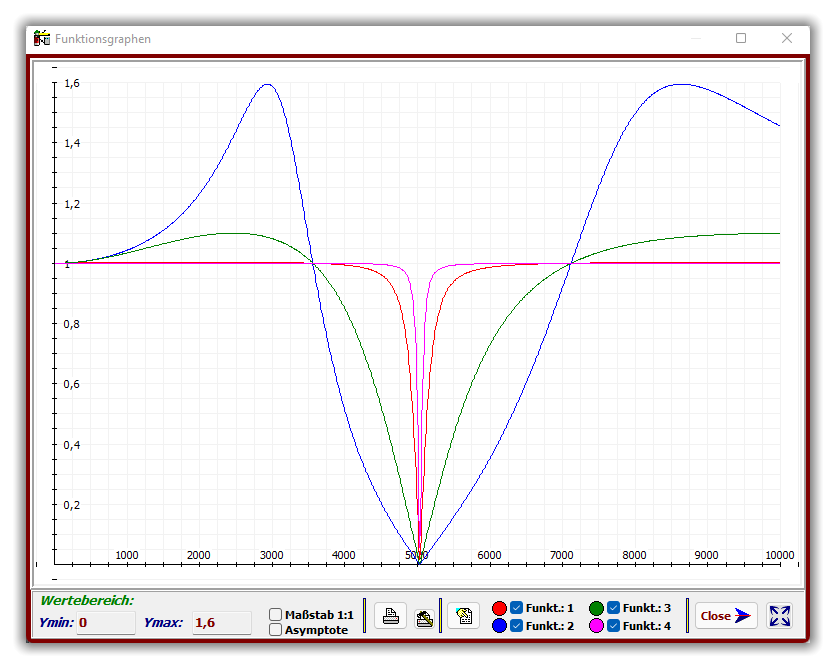
Die Kurven (grün, blau) der einzelnen Übertragungsfunktionen zeigen deutlich den Einfluss einer
Spannungsüberhöhungen (durch Fehlanpassungen) am Reihenschwingkreis.
_______________________________________________
Anregung: Wie durch die passende Veränderung der Parameter C, L und R gezeigt werden kann, zum Beispiel
in der Kombination L
2
=100 mH, C
2
=10 nF (L
1
* C
1
= L
2
* C
2
) und R
2
= 4,7 kΩ, generieren diese
Werte ebenfalls die obige rote Übertragungskurve.
Probieren Sie:
Parameter für die Funktionsgleichungen f
1
und f
2
: R → R; C → C; L → L;
Parameter für die Funktionsgleichungen f
3
und f
4
: R → W; C → A; L → B;
f
1
: |Z(x)| = {[( { R^2 + [ 2*Pi*x*L -1/(2*Pi*x*C) ]*[ 2*Pi*x*L/(1-(2*Pi*x)^2*L*C) + 2*Pi*x*L - 1/(2*Pi*x*C) ] } / { R^2
+ ( 2*Pi*x*L / (1-(2*Pi*x)^2*L*C ) + 2*Pi*x*L - 1/(2*Pi*x*C) )^2 } )^2] + [( { 2*Pi*x*R*L / (
(2*Pi*x)^2*L*C-1 ) } / { R^2 + ( 2*Pi*x*L / (1-(2*Pi*x)^2*L*C ) + 2*Pi*x*L - 1/(2*Pi*x*C) )^2 } )^2]}^0,5
f
3
: |Z(x)| = {[( { W^2 + [ 2*Pi*x*B -1/(2*Pi*x*A) ]*[ 2*Pi*x*B/(1-(2*Pi*x)^2*B*A) + 2*Pi*x*B - 1/(2*Pi*x*A) ] } / {W^2
+ ( 2*Pi*x*B / (1-(2*Pi*x)^2*B*A ) + 2*Pi*x*B - 1/(2*Pi*x*A) )^2 } )^2] + [( { 2*Pi*x*W*B / (
(2*Pi*x)^2*B*A-1 ) } / { W^2 + ( 2*Pi*x*B / (1-(2*Pi*x)^2*B*A ) + 2*Pi*x*B - 1/(2*Pi*x*A) )^2 } )^2]}^0,5
f
2
: φ*(x) = 0,005 * { arctan[ ( { 2*Pi*x*R* L / ( (2*Pi*x)^2*L*C-1 ) } / { R^2 + ( 2*Pi*x* L / (1-(2*Pi*x)^2*L* C ) +
2*Pi*x* L - 1/(2*Pi*x*C) )^2 } ) / ( { R^2 + [ 2*Pi*x* L -1/(2*Pi*x*C) ]*[ 2*Pi*x*L/(1-(2*Pi*x)^2*L*C) +
2*Pi*x* L - 1/(2*Pi*x*C) ] } / { R^2 + ( 2*Pi*x* L / (1-(2*Pi*x)^2*L* C ) + 2*Pi*x* L - 1/(2*Pi*x*C) )^2 })]}
f
4
: φ*(x) = 0,005 * { arctan[ ( { 2*Pi*x*W* B / ( (2*Pi*x)^2*B*A-1 ) } / { W^2 + ( 2*Pi*x* B / (1-(2*Pi*x)^2*B* A ) +
2*Pi*x* B - 1/(2*Pi*x*A) )^2 } ) / ( { W^2 + [ 2*Pi*x* B -1/(2*Pi*x*A) ]*[ 2*Pi*x*B/(1-(2*Pi*x)^2*B*A) +
2*Pi*x* B - 1/(2*Pi*x*A) ] } / { W^2 + ( 2*Pi*x* B / (1-(2*Pi*x)^2*B* A ) + 2*Pi*x* B - 1/(2*Pi*x*A) )^2 })]}
Beispiel (für f
1
, f
2
): R = 4700; C = 100E-9; L = 10E-3; (für f
3
, f
4
): W = 47E3; A = 10E-9; B = 100E-3
(Schalten Sie temporär f
3
und f
4
im Plotfenster aus)
Probieren Sie auch: R = 4700; C = 100e-9; L = 10e-3;
W = 2700; A= 200e-9; B = 10e-3;
Empfehlung: x ∈ [ 0; 10000 ] und y ∈ [ -0,5; 1,5 ] bzw. x ∈ [ 2000; 6000 ]


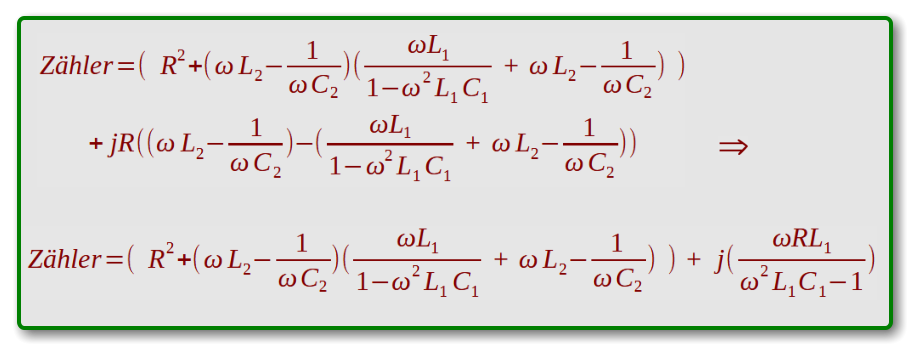

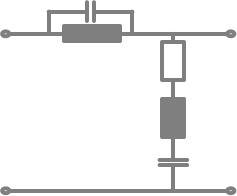
Passive Bandsperre:
Passive Bandsperre:
Ansatz und formale Berechnungen:
Ansatz und formale Berechnungen:
Formelerstellung:
Formelerstellung:

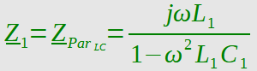

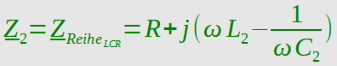


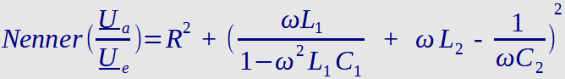
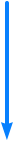
X
L1
X
L2
X
C1
X
C2
R
U
a
U
e
Formelaufbereitung für die Programmeingabe
Formelaufbereitung für die Programmeingabe


Passive Bandpässe und Bandsperren
Passive Bandpässe und Bandsperren

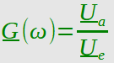
mit
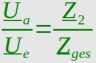
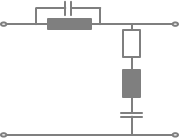
X
L1
X
L2
X
C1
X
C2
R
U
a
U
e

Realteil =
{ R^2 + [ 2*Pi*x*B -1/(2*Pi*x*A) ]*[ 2*Pi*x*L/(1-(2*Pi*x)^2*L*C) + 2*Pi*x*B - 1/(2*Pi*x*A) ] } /
{ R^2 + ( 2*Pi*x*L / (1-(2*Pi*x)^2*L*C ) + 2*Pi*x*B - 1/(2*Pi*x*A) )^2 }
Imaginärteil =
{ 2*Pi*x*R*L / ( (2*Pi*x)^2*L*C-1 ) } /
{ R^2 + ( 2*Pi*x*L / (1-(2*Pi*x)^2*L*C ) + 2*Pi*x*B - 1/(2*Pi*x*A) )^2 }
Übertragungsfunktionen in Abhängigkeit vom Widerstand R:
Übertragungsfunktionen in Abhängigkeit vom Widerstand R:
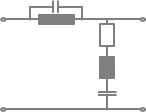
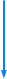
X
L1
X
L2
X
C1
X
C2
R
U
a
U
e
Filterschaltungen (aktive und passive) sperren bestimmte Frequenzbereiche aus einem breiten
Frequenzgemisch oder lassen diese durch.
Ein Bandpass (auch Bandbreitenfilter) überträgt ein nach unten und oben begrenztes
Frequenzband (f
L
-f
0
-f
H
).
Eine Bandsperre sperrt ein nach unten und oben begrenztes Frequenzband.
Passive Bandsperren bestehen nur aus passiven Bauelementen.
Ausgehend von den Formeln für idealen Parallel- und reale Reihen-
schwingkreise wird die Übertragungsfunktion erstellt.
Da u. a. der Funktionsgraf dieser Funktion vom Programm „Kleiner
Rechner“ geplottet werden soll - hier spielt die Formellänge keine
wesentliche Rolle - ist es nicht Ziel, eine bis ins Kleinste optimierte
(fehlerträchtige) Formel zu erstellen.
Übertragungsfunktion
Idealer Parallelschwingkreis
Realer Reihenschwingkreis:
(Sperrkreis)
(Saugkreis)
Da der Hauptnenner der obigen Übertragungsfunktion real ist, kann der komplexe Zähler getrennt
weiter umgeformt werden. Die Zusammenführung erfolgt nach der Zerlegung des Zählers in seine
real- und Imaginärteile.
Zur weiteren übersichtlichen Fortführung der Termumformungen werden
Zähler und Nenner der Übertragungsfunktion nun getrennt umgeformt und
anschließend wieder zusammengefügt.
Der Nenner kann als ausreichend umgeformt betrachtet werden.
Zusammenfassend gilt:
Neben der Variablen x, x = f sollen nachfolgende Parameter verwendet
werden.
Parallelschwingkreis (Z
1
)
X
C1
: C
1
[F] ⇒ C;
X
L1
: L
1
[H] ⇒ L;
Reihenschwingkreis (Z
2
)
X
C2
: C
2
[F] ⇒ A;
X
L2
: L
2
[H] ⇒ B; R [Ω] ⇒ R
____________________
Nenner
= { R^2 + ( 2*Pi*x*L / (1-(2*Pi*x)^2*L*C ) + 2*Pi*x*B - 1/(2*Pi*x*A) )^2 }
Re(Zaehler)
= { [2*Pi*x*L/(1-(2*Pi*x)^2*L*C)]*[ 2*Pi*x*L / (1-(2*Pi*x)^2*L*C) + 2*Pi*x*B - 1/(2*Pi*x*A) ] }
Im(Zaehler)
= { 2*Pi*x*R*L/(1-(2*Pi*x)^2*L*C) }
Hieraus ergeben sich für den Real- und den Imaginärteil der Übertragungsfunktion:
Der Real- und der Imaginärteil werden in die Formelgerüste eingesetzt und ergeben die direkt kopierbaren
Formeln.
f
1
: |Z(x)| = {[( { [2*Pi*x*L/(1-(2*Pi*x)^2*L*C)]*[ 2*Pi*x*L / (1-(2*Pi*x)^2*L*C) + 2*Pi*x*B - 1/(2*Pi*x*A) ] } / { R^2 + ( 2*Pi*x*L
/ (1-(2*Pi*x)^2*L*C ) + 2*Pi*x*B - 1/(2*Pi*x*A) )^2 } )^2] + [( { 2*Pi*x*R*L/(1-(2*Pi*x)^2*L*C) } / { R^2 + ( 2*Pi*x*L
/ (1-(2*Pi*x)^2*L*C ) + 2*Pi*x*B - 1/(2*Pi*x*A) )^2 } )^2]}^0,5
f
2
: |Z(x)| = {[( { [2*Pi*x*L/(1-(2*Pi*x)^2*L*C)]*[ 2*Pi*x*L / (1-(2*Pi*x)^2*L*C) + 2*Pi*x*B - 1/(2*Pi*x*A) ] } / { V^2 + ( 2*Pi*x*L
/ (1-(2*Pi*x)^2*L*C ) + 2*Pi*x*B - 1/(2*Pi*x*A) )^2 } )^2] + [( { 2*Pi*x*V*L/(1-(2*Pi*x)^2*L*C) } / { V^2 + ( 2*Pi*x*L
/ (1-(2*Pi*x)^2*L*C ) + 2*Pi*x*B - 1/(2*Pi*x*A) )^2 } )^2]}^0,5
f
3
: |Z(x)| = {[( { [2*Pi*x*L/(1-(2*Pi*x)^2*L*C)]*[ 2*Pi*x*L / (1-(2*Pi*x)^2*L*C) + 2*Pi*x*B - 1/(2*Pi*x*A) ] } / { W^2 + ( 2*Pi*x*L
/ (1-(2*Pi*x)^2*L*C ) + 2*Pi*x*B - 1/(2*Pi*x*A) )^2 } )^2] + [( { 2*Pi*x*W*L/(1-(2*Pi*x)^2*L*C) } / { W^2 + ( 2*Pi*x*L
/ (1-(2*Pi*x)^2*L*C ) + 2*Pi*x*B - 1/(2*Pi*x*A) )^2 } )^2]}^0,5
Werte
X
L1
: L
1
= 10 mH (10e-3 H ) → L = 10E-3; X
C1
: C
1
= 100 nF (100e-9 F) → C = 100E-9;
X
L2
: L
2
= 10 mH
→ B = 10E-3; X
C2
: C
2
= 100 nF
→ A = 100E-9;
Parameter R:
R
r
= 1,2 kΩ (rot)
R = 1200;
R
b
= 4,7 kΩ (blau)
V = 4700;
R
g
= 320 Ω (grün)
W = 320;
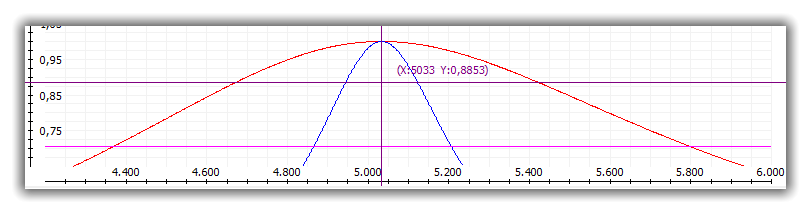
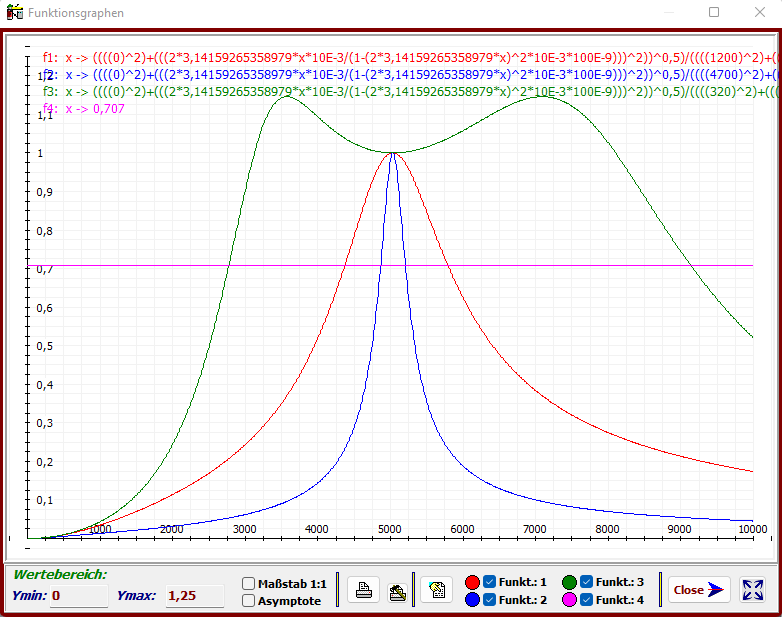
Die obigen Übertragungsfunktionen zeigen drei Bandpässe mit der Mittelfrequenz f
0
= 5033 Hz. Die
Kondensatoren und Spulen haben gleiche Werte (L
1
=L
2
; C
1
=C
2
). Experimente mit unterschiedlichen
Werte (L
1
≠L
2
; C
1
≠C
2
usw.) bieten sich hier an.
Aus den Spreizungen der Kurven lassen sich die folgenden Werte ablesen:
für R = 1,2 kΩ → f
L
= 4372 Hz; f
0
= 5033 Hz; f
H
= 5793 Hz
für R = 4,7 kΩ → f
L
= 4865 Hz; f
0
= 5033 Hz; f
H
= 5205 Hz
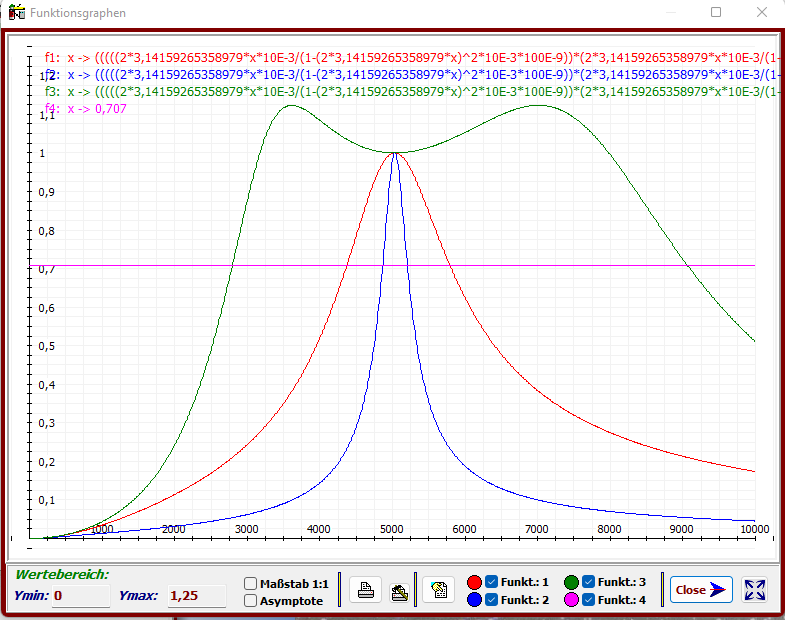
Hier werden einmal die (obige) Übertragungsfunktion incl. ihrer Real- und Imaginärteile als
Funktionsgraphen zur Übersicht bzw. zur Untersuchung ausgegeben.
f
1
: |Z(x)| = {[( { [2*Pi*x*L/(1-(2*Pi*x)^2*L*C)]*[ 2*Pi*x*L / (1-(2*Pi*x)^2*L*C) + 2*Pi*x*B - 1/(2*Pi*x*A) ] } / { R^2 + ( 2*Pi*x*L
/ (1-(2*Pi*x)^2*L*C ) + 2*Pi*x*B - 1/(2*Pi*x*A) )^2 } )^2] + [( { 2*Pi*x*R*L/(1-(2*Pi*x)^2*L*C) } / { R^2 + ( 2*Pi*x*L
/ (1-(2*Pi*x)^2*L*C ) + 2*Pi*x*B - 1/(2*Pi*x*A) )^2 } )^2]}^0,5
f
2
: Im(Z) = { 2*Pi*x*R*L/(1-(2*Pi*x)^2*L*C) } / { R^2 + ( 2*Pi*x*L / (1-(2*Pi*x)^2*L*C ) + 2*Pi*x*B - 1/(2*Pi*x*A) )^2 }
f
3
: Re(Z) = { [2*Pi*x*L/(1-(2*Pi*x)^2*L*C)]*[ 2*Pi*x*L / (1-(2*Pi*x)^2*L*C) + 2*Pi*x*B - 1/(2*Pi*x*A) ] } / { R^2 + ( 2*Pi*x*L /
(1-(2*Pi*x)^2*L*C ) + 2*Pi*x*B - 1/(2*Pi*x*A) )^2 }
Werte:
X
L1
: L
1
= 10 mH → L = 10e-3; X
C1
: C
1
= 100 nF → C = 100e-9;
X
L2
: L
2
= 10 mH → B = 10e-3; X
C2
: C
2
= 100 nF → A = 100e-9;
R = 1,2 kΩ → R 1200;
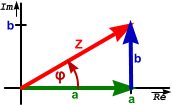
Die Kurven zeigen die zur jeweiligen Frequenz zugehörigen Vektorenlän-
gen des Summenvektors Z = [a
2
+b
2
]
0,5
, des Realteilvektors a = Re(Z) und
des Imaginärteilvektors b = Im(Z) an.

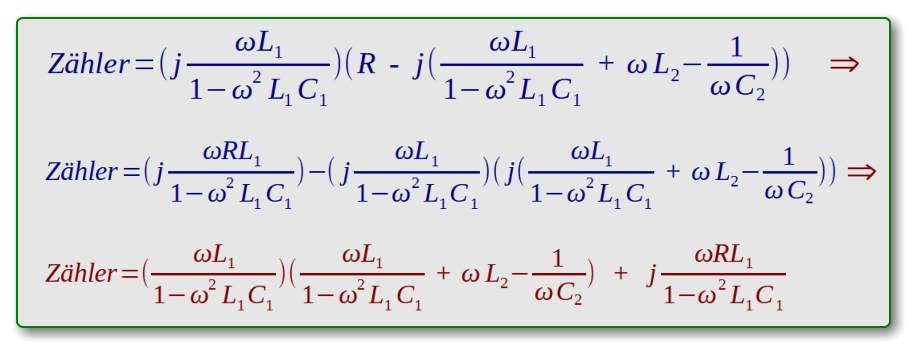

Passiver Bandpass:
Passiver Bandpass:

Ansatz und formale Berechnungen:
Ansatz und formale Berechnungen:
Formelerstellung:
Formelerstellung:

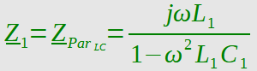

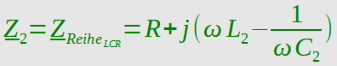


Formelaufbereitung für die Programmeingabe
Formelaufbereitung für die Programmeingabe


Passive Bandpässe und Bandsperren
Passive Bandpässe und Bandsperren
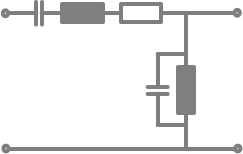

X
L1
X
L2
X
C1
X
C2
R
U
a
U
e

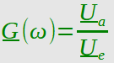
mit
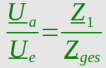
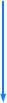
X
L1
X
L2
X
C1
X
C2
R
U
a
U
e

Realteil =
{ [2*Pi*x*L/(1-(2*Pi*x)^2*L*C)]*[ 2*Pi*x*L / (1-(2*Pi*x)^2*L*C) + 2*Pi*x*B - 1/(2*Pi*x*A) ] } /
{ R^2 + ( 2*Pi*x*L / (1-(2*Pi*x)^2*L*C ) + 2*Pi*x*B - 1/(2*Pi*x*A) )^2 }
Imaginärteil =
{ 2*Pi*x*R*L/(1-(2*Pi*x)^2*L*C) } /
{ R^2 + ( 2*Pi*x*L / (1-(2*Pi*x)^2*L*C ) + 2*Pi*x*B - 1/(2*Pi*x*A) )^2 }
Real- und Imaginärteile der Übertragungsfunktion
Real- und Imaginärteile der Übertragungsfunktion


Realteil =
{ [2*Pi*x*L/(1-(2*Pi*x)^2*L*C)]*[ 2*Pi*x*L / (1-(2*Pi*x)^2*L*C) + 2*Pi*x*B - 1/(2*Pi*x*A) ] } /
{ R^2 + ( 2*Pi*x*L / (1-(2*Pi*x)^2*L*C ) + 2*Pi*x*B - 1/(2*Pi*x*A) )^2 }
Imaginärteil =
{ 2*Pi*x*R*L/(1-(2*Pi*x)^2*L*C) } /
{ R^2 + ( 2*Pi*x*L / (1-(2*Pi*x)^2*L*C ) + 2*Pi*x*B - 1/(2*Pi*x*A) )^2 }
Ein Vorteil der Polarform sind u. a. die (relativ) einfachen Berechnungen von Produkten und
Quotienten. Dieses kann bei der Aufstellung der Übertragungsfunktion zu vereinfachten
Rechnungen führen.
Ausgehend von den Formeln für idealen Parallel- und reale Reihen-
schwingkreise wird die Übertragungsfunktion erstellt (siehe auch LC-
Bandpass).
Übertragungsfunktion
Komplexe Widerstände
Zur Berechnung der Übertragungsfunktionskurve |G(x)| und der Phasengangkurve werden die
Real- und Imaginärteile des komplexen Gesamtwiderstandes und des Widerstandes Z1 benötigt.
Neben der Variablen x, x = f sollen nachfolgende Parameter verwendet werden.
Parallelschwingkreis (Z
1
):
C
1
[F] ⇒ C; L
1
[H] ⇒ L;
Reihenschwingkreis (Z
2
):
C
2
[F] ⇒ A; L
2
[H] ⇒ B; R [Ω] ⇒ R
(Reihenschaltung Saugkreis + Sperrkreis)
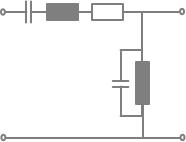
|G(x)| = |Z1(x)| / |Zges(x)|
f
1
: |G(x)| = [ {[( 0 )^2] + [( { 2*Pi*x*L / (1-(2*Pi*x)^2*L*C) } )^2]}^0,5 ] /
[ {[( R )^2] + [( { 2*Pi*x*L / (1-(2*Pi*x)^2*L*C ) + 2*Pi*x*B - 1/(2*Pi*x*A) } )^2]}^0,5 ]
Zur Darstellung der Graphen f
2
und f
3
(Parameter U und V statt R):
f
2
: |G(x)| = [ {[( 0 )^2] + [( { 2*Pi*x*L / (1-(2*Pi*x)^2*L*C) } )^2]}^0,5 ] /
[ {[( V )^2] + [( { 2*Pi*x*L / (1-(2*Pi*x)^2*L*C ) + 2*Pi*x*B - 1/(2*Pi*x*A) } )^2]}^0,5 ]
f
3
: |G(x)| = [ {[( 0 )^2] + [( { 2*Pi*x*L / (1-(2*Pi*x)^2*L*C) } )^2]}^0,5 ] /
[ {[( W )^2] + [( { 2*Pi*x*L / (1-(2*Pi*x)^2*L*C ) + 2*Pi*x*B - 1/(2*Pi*x*A) } )^2]}^0,5 ]
Werte:
X
L1
: L
1
= 10 mH → L = 10E-3; X
C1
: C
1
= 100 nF → C = 100E-9;
X
L2
: L
2
= 10 mH → B = 10E-3; X
C2
: C
2
= 100 nF → A = 100E-9;
R
f1
= 1,2 kΩ (rot)
→ R = 1200;
R
f2
= 4,7 kΩ (blau) → V = 4700;
R
f3
= 320 Ω (grün) → W = 320;
Reesüme: Wie das Beispiel zeigt, können gezielte Verwendungen der Polarformen oft zu
einfacheren und schnelleren Umformungen führen.

Passiver Bandpass:
Passiver Bandpass:

Ansatz und formale Berechnungen:
Ansatz und formale Berechnungen:
Formelerstellung:
Formelerstellung:

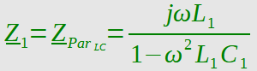

Vorbetrachtungen
Vorbetrachtungen


X
L1
X
L2
X
C1
X
C2
R
U
a
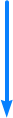
U
e
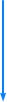
X
L1
X
L2
X
C1
X
C2
R
U
a
U
e

Formelaufbereitung für die Programmeingabe
Formelaufbereitung für die Programmeingabe

Realteil
= 0
Imaginärteil
= { 2*Pi*x*L / (1-(2*Pi*x)^2*L*C) }

Realteil
= R
Imaginärteil
= { 2*Pi*x*L / (1-(2*Pi*x)^2*L*C ) + 2*Pi*x*B - 1/(2*Pi*x*A) }
Widerstand Z1 des parallelen Schwingkreises (Sperrkreis):
Widerstand Z1 des parallelen Schwingkreises (Sperrkreis):
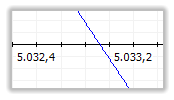
Gesamtwiderstand Z
ges
der Schaltung:
Gesamtwiderstand Z
ges
der Schaltung:
Für die Übertragungsfunktion gilt nun:
Für die Übertragungsfunktion gilt nun: